AT_tenka1_2015_qualA_e 天下一魔法使い
题目描述
为了成为天下第一的魔法师,你正在练习把魔法阵画在地上。下面是魔法阵的描绘方法:
- 在圆周上等距画 $N$ 个点,使其中一个点位于正北的位置
- 把点连接成线段,画若干个**有 $K$ 个以上顶点的不自交**的多边形。
- 每个点必须被一个且仅被一个多边形包含
- 画出的多边形必须连成一条线。我们定义:连成一条线是指,对于任意一对多边形 $(A, B)$,这两个多边形都被连接。另外,多边形$A$和多边形$B$连接,是指满足以下任一条件的状态:
1. 多边形 $A$ 的边和多边形 $B$ 的边在 $1$ 处以上交叉。
2. 存在多边形 $C$,其中多边形 $A$ 和多边形 $C$ 连接,并且多边形 $B$ 和多边形 $C$ 连接。
例如,当 $N=10$,$K=3$ 的时候可以画以下的魔法阵:
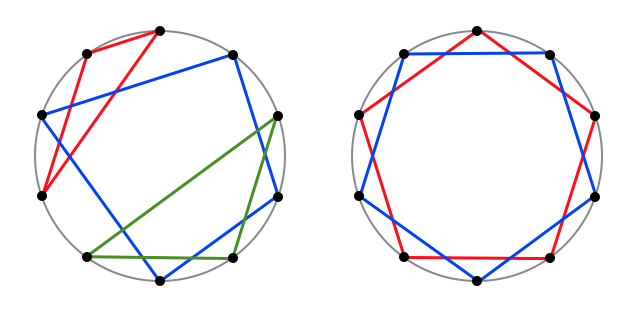
以下的魔法阵,因为所有多边形没有连接在一起,所以不是正确的魔法阵。
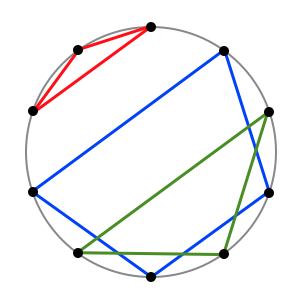
你决定计算一下可以画出多少符合条件的魔法阵。
输入格式
标准输入,格式如下:
$N$ $K$
在第 $1$ 行中,给出 $2$ 个整数:$N(3≤N≤400),K(3≤K≤N)$,以空格隔开。
输出格式
输出一行,表示符合条件的魔法阵的个数,由于结果可能较大,你需要将答案对于$1000000007(1e9+7)$ 取模。
### 输入输出样例
上方已经给出。
说明/提示
#### 部分分
这个问题设置了部分分数点。
对于 $30\%$ 的分数点,满足:$N≤50, K=N/3$。
对于 $50\%$ 的分数点,满足:$N≤50$。
对于 $100\%$ 的分数点,满足:$3≤N≤400,3≤K≤N$。
##### 样例1:
你可以画以下八种魔法阵:
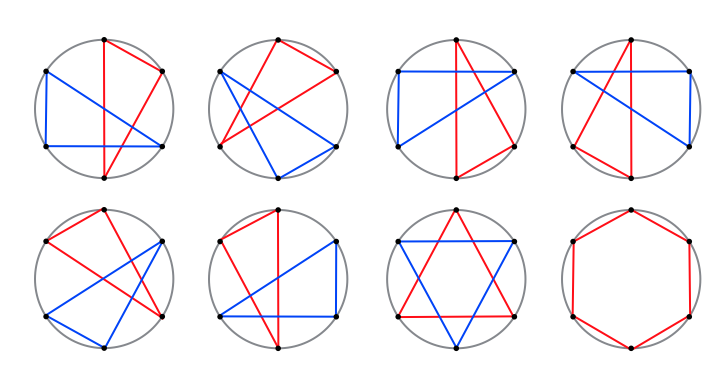
##### 样例2:
只能画六角形的图案。