AT_tenka1_2015_qualA_e 天下一魔法使い

[problemUrl]: https://atcoder.jp/contests/tenka1-2015-quala/tasks/tenka1_2015_qualA_e あなたは天下一の魔法使いになるために、魔法陣を地面に描く練習をしています。魔法陣の描き方は以下の通りです。 - 円周上に $ N $ 個の点を等間隔に、点のうちの $ 1 $ つが真北の位置になるように描く。 - 点を線分でつないで、$ K $ 頂点以上の自己交差のない多角形をいくつか描く。 - 各点がちょうど $ 1 $ つの多角形に含まれるようにしなければならない。 - 描かれた多角形がひとつながりになっていなければならない。ただし、多角形がひとつながりになっているとは、全ての多角形のペア $ (a,\ b) $ について、多角形 $ a $ と多角形 $ b $ が連結であるような状態を指す。また、多角形 $ a $ と多角形 $ b $ が連結であるとは、以下のいずれかの条件を満たすような状態を指す。 - 多角形 $ a $ の辺と多角形 $ b $ の辺が $ 1 $ 箇所以上で交差している。 - 多角形 $ a $ と多角形 $ c $ が連結かつ多角形 $ b $ と多角形 $ c $ が連結であるような多角形 $ c $ が存在する。 例えば、$ N\ =\ 10,\ K\ =\ 3 $ のときは以下のような魔法陣を描くことができます。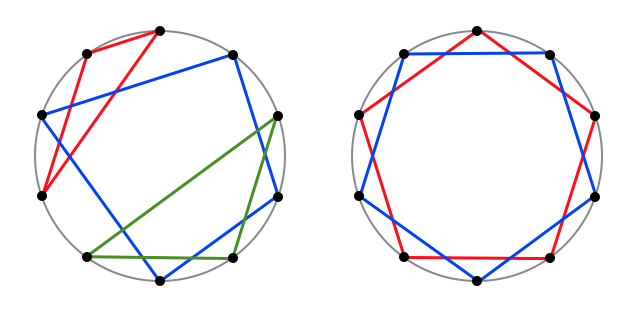 以下のような魔法陣は、多角形がひとつながりになっていないため正しい魔法陣ではありません。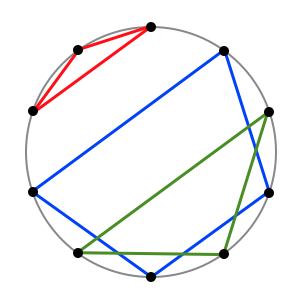 あなたは、このような方法で描くことができる魔法陣がいくつあるのか計算してみることにしました。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ K $ - $ 1 $ 行目に、$ 2 $ つの整数 $ N\ (3\ ≦\ N\ ≦\ 400),\ K\ (3\ ≦\ K\ ≦\ N) $ が空白区切りで与えられる。

問題文の方法で描くことのできる魔法陣の個数を $ 1,000,000,007\ (10^9+7) $ で割った余りを $ 1 $ 行に出力せよ。出力の末尾に改行を入れること。

### 配点 この問題には部分点が設定されている。 - $ N\ ≦\ 50 $ かつ $ N/3\ を満たすテストケース全てに正解した場合は、30 $ 点が与えられる。 - $ N\ ≦\ 50 $ を満たすテストケース全てに正解した場合は、上記とは別に $ 50 $ 点が与えられる。 - 全てのテストケースに正解した場合は、上記とは別に $ 50 $ 点が与えられる。 ### Sample Explanation 1 以下の $ 8 $ 通りの魔法陣を描くことができます。 !\[fig3\](https://tenka1-2015-quala.contest.atcoder.jp/img/other/tenka1\_2015\_quala/xvcbkasdkhjer/fig3.png) ### Sample Explanation 2 六角形を描くパターンだけが描けます。