AT_tenka1_2016_qualA_e 無限グラフ
题目描述
*天下一研究所作为组合数学的研究基地,正在开展各种活动。最近,关于拥有无限个顶点的图的研究似乎非常活跃。*
给定一个正整数 $N$,以及 $M$ 对整数对 $(A_1, B_1), (A_2, B_2), \ldots, (A_M, B_M)$,其中每个整数满足 $0 \leq A_i, B_i \leq N-1$。
我们考虑如下的一个拥有无限个顶点的无向图:
- 对于任意整数 $z$(包括负整数),存在唯一一个与之对应的顶点。我们称与整数 $z$ 对应的顶点为顶点 $z$。不存在与某个整数不对应的顶点。
- 对于任意 $i$($1 \leq i \leq M$)和任意整数 $k$,顶点 $A_i + k \times N$ 与顶点 $B_i + (k+1) \times N$ 之间有一条无向边。除此之外,不存在其他边。
(请参考输入输出示例部分的图片)
请判断该图的连通分量个数是否有限。如果有限,请求出其个数。
输入格式
输入以如下格式从标准输入给出。
> $N$ $M$ $A_1$ $B_1$ $A_2$ $B_2$ $\ldots$ $A_M$ $B_M$
输出格式
如果给定的图的连通分量个数有限,则输出该个数。如果无限,则输出 $-1$。
说明/提示
### 限制
- $1 \leq N \leq 10^5$
- $1 \leq M \leq 10^5$
- $0 \leq A_i, B_i \leq N-1$
- 所有的 $(A_i, B_i)$ 均互不相同。
### 部分得分
- 有 $400$ 分的数据满足:
- $1 \leq N \leq 1000$
- $1 \leq M \leq 1000$
### 样例解释 1
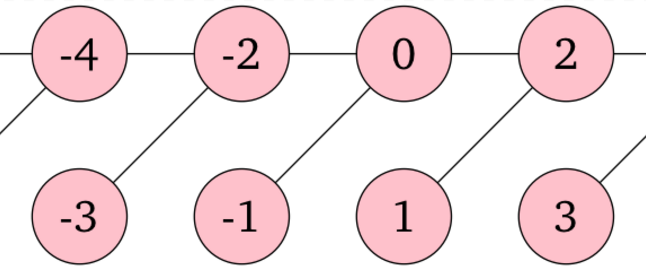 沿着边可以在任意两个顶点之间往返。因此,该图的连通分量个数为 $1$。
### 样例解释 2
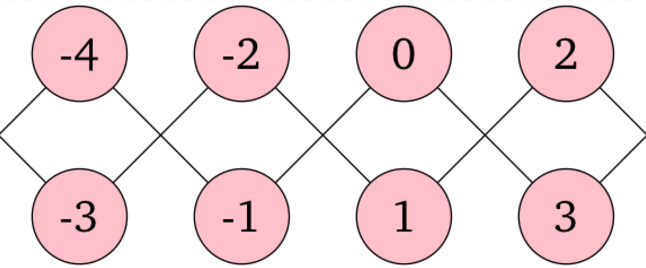 存在 $2$ 个无限长的线性连通分量。
### 样例解释 3
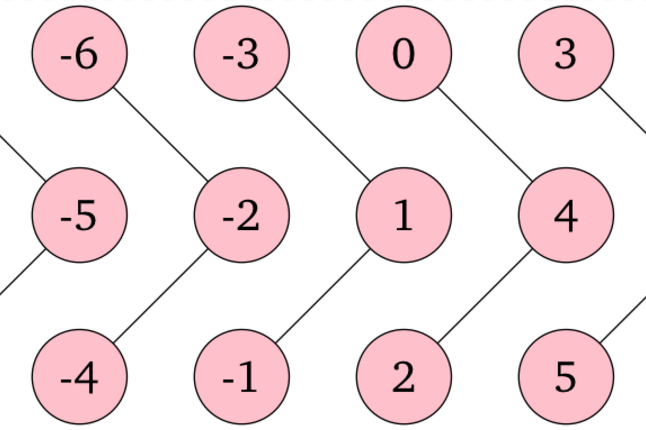 存在无限多个由 $3$ 个顶点组成的连通分量。
由 ChatGPT 4.1 翻译