AT_tkppc3_d 巨大チェスボード

[problemUrl]: https://atcoder.jp/contests/tkppc3/tasks/tkppc3_d 配点： $ 400 $ 点 ZRK 君は誕生日に Mr.RKZ からチェスボードをもらった. そのチェスボードは縦 $ H $ マス \* 横 $ W $ マスとなっており, 全ての辺は外枠と並行もしくは直交している. 上から $ i $ 行目, 左から $ j $ 列目のマスをマス $ (i,\ j) $ とする. また, チェスボードのマス $ (1,\ 1) $ は黒く, 隣り合うマスには異なる色が塗られるように, 下図のように色が塗られている. しかし, そのチェスボードはマス目の大きさがゆがんでおり, 上から $ i $ 行目のマスは全て高さが $ a_i $, 左から $ j $ 列目のマスは全て幅が $ b_j $ となっている. （詳しくは下の図を参考にすること.） 不良品をもらってしまった ZRK 君は, 「左上のマスが $ (px,\ py) $ で右下のマスが $ (qx,\ qy) $ である長方形に含まれる, (黒い長方形の面積の合計) - (白い長方形の面積の合計)」を $ Q $ 回求める遊びをすることで心を落ち着けることにした. 怒っている ZRKのために, その答えを求めよ. 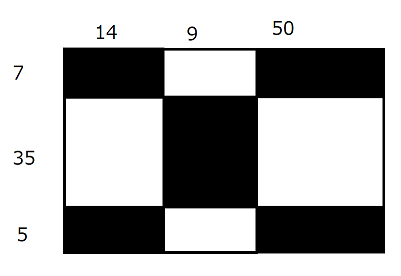以下は, $ a_1=7,\ a_2=35,\ a_3=5,\ b_1=14,\ b_2=9,\ b_3=50 $ の場合のチェスボードの図である. 

入力は以下の形式で標準入力から与えられる. > $ H $ $ W $ $ Q $ $ a_1 $ $ a_2 $ $ a_3 $ ... $ a_H $ $ b_1 $ $ b_2 $ $ b_3 $ ... $ b_W $ $ px_1 $ $ py_1 $ $ qx_1 $ $ qy_1 $ $ px_2 $ $ py_2 $ $ qx_2 $ $ qy_2 $ $ px_3 $ $ py_3 $ $ qx_3 $ $ qy_3 $ ... $ px_Q $ $ py_Q $ $ qx_Q $ $ qy_Q $

$ Q $ 行にわたって出力せよ. $ i $ 行目には, 左上のマスが $ (px_i,\ py_i) $, 右下のマスが $ (qx_i,\ qy_i) $ である長方形に含まれる (黒い長方形の面積の合計) - (白い長方形の面積の合計) を出力せよ.

### 制約 - $ H,\ W,\ Q $ は $ 1 $ 以上 $ 100\ 000 $ 以下の整数である. - $ a_i,\ b_i $ は $ 1 $ 以上 $ 10\ 000 $ 以下の整数である. - $ px_i,\ qx_i $ は $ 1 $ 以上 $ H $ 以下の整数である. - $ py_i,\ qy_i $ は $ 1 $ 以上 $ W $ 以下の整数である. - $ px_i\ \leq\ qx_i $, $ py_i\ \leq\ qy_i $ である. ### 小課題 小課題1 \[ $ 30 $点 \] - $ H,\ W\ \leq\ 1\ 000 $ を満たす. - $ Q\ \leq\ 5 $ を満たす. 小課題2 \[ $ 120 $点 \] - $ H,\ W\ \leq\ 1\ 000 $ を満たす. 小課題3 \[ $ 250 $点 \] - 追加の制約はない.