AT_tkppc4_2_a Jumping!!

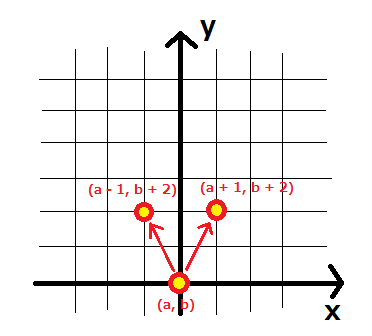
[problemUrl]: https://atcoder.jp/contests/tkppc4-2/tasks/tkppc4_2_a 配点 $ 200 $ 点 座標平面上にAliceがいます。彼女のいる座標は $ (0,0) $ です。 彼女は「桂馬飛び」のみで座標 $ (x,y) $ に行けるでしょうか。行ける場合は、最小で何回の桂馬飛びで行けるのかを求めてください。 なお、$ 1 $ 回の「桂馬飛び」とは以下の移動のことを指します。 - 座標 $ (a,b) $ にいる時、座標 $ (a+1,b+2) $ または $ (a-1,b+2) $ に移動する。 

入力は以下の形式で標準入力から与えられます。 > $ x $ $ y $

座標 $ (x,y) $ に行ける場合は、最小で何回の桂馬飛びをするかを出力してください。行けない場合は $ -1 $ を出力してください。

### 制約 - 入力は全て整数である。 - $ -10^5\ \leq\ x,\ y\ \leq\ 10^5 $ ### Sample Explanation 1 $ 1 $ 回目で $ (1,2) $ に飛び、$ 2 $ 回目で $ (0,4) $ に飛び、$ 3 $ 回目で $ (1,6) $ に飛ぶことでたどり着けます。 以下の画像のように動きます。 !\[\](https://img.atcoder.jp/tkppc4-2/1a9d0ec0c05411619f92b013a90c95b4.png) ### Sample Explanation 2 どのように動いても、座標 $ (6,\ 1) $ には桂馬飛びだけではたどり着けません。