AT_tkppc4_2_l 建物と魔女

[problemUrl]: https://atcoder.jp/contests/tkppc4-2/tasks/tkppc4_2_l **この問題はインタラクティブ問題ですので、通常の問題と形式が異なります。ご注意ください。** パ研王国には、$ N $ 個の都市があります。また、$ N\ -\ 1 $ 本の双方向を繋ぐ道で結ばれており、これらの道のみを使って任意の都市から任意の都市までを移動することが出来ます。すなわち、パ研王国は「木構造」を成します。 また各都市には、都市を代表する建物が $ 1 $ 個ずつあります。 さて、E869120 君はパ研王国の構造、すなわちパ研王国の各道がどの都市とどの都市の間を繋いでいるのかを知りたいですが、パ研王国は魔の手により封鎖されているため簡単に知る事は出来ません。 そこで、パ研王国の大統領である魔女の Segtree さんに以下の質問をすることによって、パ研王国の構造を知ろうとしました。 - 長さ $ N $ の順列 $ p $ を指定する。ここで、$ p $ は $ 1 $ 以上 $ N $ 以下の値が $ 1 $ 個ずつ含まれているものでなければならない。 - Segtree さんに魔力を使ってもらい、都市 $ i $ を代表する建物の高さを $ 2^{p_i\ -\ 1} $ に設定してもらう。 - そして、$ 0 $ 以上 $ 2^{N}-1 $ 以下の値 $ x $ を指定し、以下の条件を満たす $ (u,\ v) $ ($ u\ )\ の組の個数\ e $ を答えてもらう。 - $ u $ から $ v $ までの最短経路において、通る都市の建物の高さの合計が $ x $ 以上であるようなもの。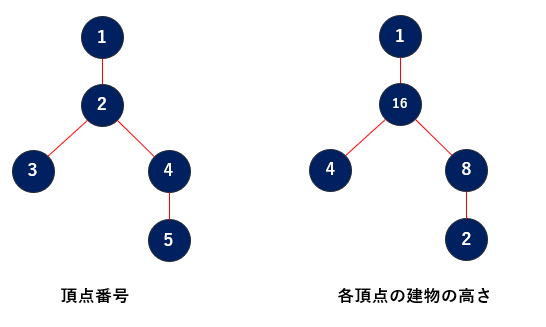 例えば、パ研王国が以下の図のような構造である場合において、$ p\ = $ {$ 1,\ 5,\ 3,\ 4,\ 2 $}, $ x\ =\ 21 $ の場合、 - まず、各都市の建物の高さは下図の通り、{$ 1,\ 16,\ 4,\ 8,\ 2 $} となります。 - よって、$ (u,\ v)\ =\ (1,\ 3),\ (1,\ 4),\ (1,\ 5),\ (2,\ 4),\ (2,\ 5),\ (3,\ 4),\ (3,\ 5) $ の $ 7 $ 通りにおいて $ x\ \geq\ 21 $ の条件を満たすため、魔女の Segtree さんは$ 7 $ を返します。 - 例えば、$ 1 $ から $ 5 $ までの最短経路において通る都市の建物の高さの合計は、$ 1 $ (都市 $ 1 $) + $ 16 $ (都市 $ 2 $) + $ 8 $ (都市 $ 4 $) + $ 2 $ (都市 $ 5 $) = $ 27 $ となり、$ 21 $ 以上であるため条件を満たします。  E869120 君は魔女の Segtree さんに質問しすぎると、パ研王国の軍隊に襲われる可能性が高まるため、出来るだけ少ない質問回数でパ研王国の構造を知りたいです。特に、$ 3\ 600 $ 回を超えて質問した場合、軍隊だけでなく Segtree さんも怒り狂い、自動的に不正解となります。 ですが彼にとってこの問題は難しすぎて解けません。彼の代わりにできるだけ少ない質問回数で構造を当てるプログラムを作成して下さい。 ### Input & Output Format **この問題はインタラクティブ問題であるため、通常の入出力形式とは違います。ご注意ください。** (△) まず、ジャッジから都市の数 $ N $ を以下の形式で受け取ります。 > $ N $ 次に、(☆) と (★) の入出力を、パ研王国の構造が分かるまで繰り返し行います。 (☆) 自分が魔女 (ジャッジ) に対して質問を以下の形式で行います。 > ? $ p_1 $ $ p_2 $ $ p_3 $ ... $ p_N $ $ x $ このように、最初に `'?'` を出力し、その後 $ N\ +\ 1 $ 個の整数を出力してください。その際、出力は `?` を含め全て一行で行ってください。なお、$ p,\ x $ の値に関しては問題文を参照してください。 また、$ p $ は $ 1 $ 以上 $ N $ 以下の値を $ 1 $ 回ずつ含む順列である必要があり、$ x $ は $ 0 $ 以上 $ 2^{N}-1 $ 以下の値である必要があります。 最後に改行を忘れないようにしてください。 (★) 魔女 (ジャッジ) が質問に対する回答を行います。 回答は、$ 1 $ つの整数 $ e $ で表されます。ジャッジに質問をしたら、$ 1 $ つの整数を受け取るようにしてください。 **ただし、$ 3\ 600 $ 回を超える質問をした場合、$ -1 $ という値を返します。この場合、直ちにプログラムを終了させてください。質問制限回数を超えた場合にプログラムを終了させたときの挙動は WA となりますが、プログラムを終了しない場合の挙動は定義されていません。** (◇) 答えとなるパ研王国の構造が分かったら、以下のように出力してください。 > ! $ a_1 $ $ b_1 $ $ a_2 $ $ b_2 $ $ a_3 $ $ b_3 $ ... $ a_{N-1} $ $ b_{N-1} $ このように、$ N $ 行に渡って出力してください。 ただし、$ a_i $, $ b_i $ は、パ研王国の構造を表す値です。具体的には、$ i $ 本目の道路が $ a_i $ と $ b_i $ を結んでいるという事を指します。 道路を出力する順番はどれでも構いません。また、$ a_i,\ b_i $ の順番が逆でも構いません。例えば、パ研王国の道が $ (1,\ 2),\ (2,\ 3),\ (3,\ 4) $ であった時に、以下のような出力をしても正解となります。 ``` 3 2 1 2 4 3 ```

N/A

N/A

### 制約 - $ 1\ \leq\ N\ \leq\ 60 $ - パ研王国は連結な木構造を成す。つまり、任意の都市から任意の都市まで道を辿って行くことが出来る。 ### 小課題 この課題には、$ 2 $ 個の小課題があります。 1. (100 点) $ N\ \leq\ 4 $ を満たす。 2. (1200 点) $ 5\ \leq\ N\ \leq\ 60 $ を満たす。 ただし、小課題 $ 2 $ においては、質問回数の最大値 $ Q $ によって得点が決まります。 質問回数の最大値 $ Q $ 小課題 $ 2 $ の得点 ($ 1\ 200 $ 点満点) $ 2\ 001\ \leq\ Q\ \leq\ 3\ 600 $ $ 310 $ $ 1\ 721\ \leq\ Q\ \leq\ 2\ 000 $ $ 420 $ $ 1\ 101\ \leq\ Q\ \leq\ 1\ 720 $ $ 550 $ $ 601\ \leq\ Q\ \leq\ 1\ 100 $ $ 1\ 200\ -\ (Q\ -\ 600) $ $ Q\ \leq\ 600 $ $ 1\ 200 $### 注意 **出力形式を間違えた場合のジャッジの挙動は不定です。(WA とは限りません。)** **また、出力の最後に flush しなければならず、そうしない場合 TLE となる場合がございます。** **E869120 君 は、$ 3\ 600 $ 回を超える質問をしてはなりません。この回数の質問を超えてもなおプログラムを打ち切らない場合の挙動は不定です。** **なお、AC となった場合でも満点が取れていない場合があることにご注意ください。小課題 $ 1 $, $ 2 $ 全てのテストケースにおいて $ 3\ 600 $ 回以内の質問で答えが求まれば、たとえ部分点であっても AC と出ます。** ### 入出力例 1 この入力例は、$ N\ =\ 4 $ であり、パ研王国が以下のような構造である場合のジャッジ側とのやり取りの例である。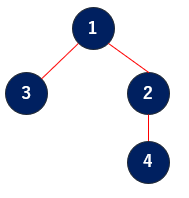  自分のプログラムへの入力（ジャッジ側の出力） 自分のプログラムの出力 4 ? 1 2 3 4 8 3 ? 4 3 2 1 15 1 ! 1 2 2 4 1 3