AT_toyota_hc_2023spring_a Container Loading

トヨタ自動車株式会社では、たくさんの荷物をコンテナに入れて運んでいる。 荷物の集合とコンテナのサイズのデータが与えられるので、全ての荷物をコンテナに上手く積み込む方法を出力せよ。 荷物を積み込む順番は任意ではあるが、積み込み作業の効率化のため、出来るだけ順番通りに積んで欲しい。

入力は以下の形式で標準入力から与えられる。 $ w, h $ の順序が誤っていたため、修正を行いました。tools類への修正を省くため、 $ W, H $ の順序と対応が逆になり紛らわしくなりますが、以下のようにコンテナサイズは $ W H $ の順、荷物のサイズは $ h w $ の順になります。csvファイルは $ w,h,d $ の順となっています。 > $ M $ $ W $ $ H $ $ B $ $ D $ > $ h_0 $ $ w_0 $ $ d_0 $ $ a_0 $ $ f_0 $ $ g_0 $ > $ h_1 $ $ w_1 $ $ d_1 $ $ a_1 $ $ f_1 $ $ g_1 $ > : > $ h_{M-1} $ $ w_{M-1} $ $ d_{M-1} $ $ a_{M-1} $ $ f_{M-1} $ $ g_{M-1} $ - 荷物の種類数 $ M $ は、 $ 1 $ 以上の整数である。 - コンテナと四隅のブロックの大きさは $ W = 1120 $ 、 $ H = 680 $ 、 $ B = 30 $ 、 $ D\in\{600,1200\} $ を満たす。 - 各荷物の大きさ $ (w_i,h_i,d_i) $ の組み合わせは [このcsvファイル](https://img.atcoder.jp/toyota-hc-2023spring/d1cb95b8.csv) に記されているもののいづれかに一致する。 - 荷物の個数 $ a_i $ は $ 1 $ 以上 $ 30 $ 以下の整数である。 - 荷物の回転制限フラグ $ f_i $ 及び上への積み重ね制限フラグ $ g_i $ は `Y` もしくは `N` のいづれかである。

横方向に $ x $ 軸、縦方向に $ y $ 軸、高さ方向に $ z $ 軸を取る。 コンテナの占める領域(ブロック部分を含む)は $ [0,W]\times[0,H]\times[0,D] $ である。 荷物の総数を $ N=\sum_{i=0}^{M-1} a_i $ とする。 $ i $ 番目に積む荷物の種類を $ p_i $ ( $ 0\leq p_i\leq M-1 $ ) とする。 $ i $ 番目に積む荷物の配置は、荷物の角のうちで原点に最も近い点の座標 $ (x_i,y_i,z_i) $ と以下のように定める向き $ r_i $ によって表現することにする。 - $ r_i = 0 $ の時、横 $ (w_{p_i}) $ の辺が横軸、縦 $ (h_{p_i}) $ の辺が縦軸に平行になるように置く。 - $ r_i = 1 $ の時、縦 $ (h_{p_i}) $ の辺が横軸、横 $ (w_{p_i}) $ の辺が縦軸に平行になるように置く。 - $ r_i = 2 $ の時、高さ $ (d_{p_i}) $ の辺が横軸、縦 $ (h_{p_i}) $ の辺が縦軸に平行になるように置く。 - $ r_i = 3 $ の時、縦 $ (h_{p_i}) $ の辺が横軸、高さ $ (d_{p_i}) $ の辺が縦軸に平行になるように置く。 - $ r_i = 4 $ の時、高さ $ (d_{p_i}) $ の辺が横軸、横 $ (w_{p_i}) $ の辺が縦軸に平行になるように置く。 - $ r_i = 5 $ の時、横 $ (w_{p_i}) $ の辺が横軸、高さ $ (d_{p_i}) $ の辺が縦軸に平行になるように置く。 例えば、 $ r_i=0 $ のとき、荷物の占める領域は $ [x_i,x_i+w_{p_i}]\times[y_i,y_i+h_{p_i}]\times[z_i,z_i+d_{p_i}] $ となる。 $ f_{p_i} $ が `N` である荷物 $ i $ は底面を固定した回転しか許されないため、 $ r_i $ の値は $ 0 $ か $ 1 $ でなければならない。 また、 $ (x_i,y_i,z_i) $ は整数座標でなければならない。 このとき、以下の形式で標準出力に出力せよ。 > $ p_0 $ $ r_0 $ $ x_0 $ $ y_0 $ $ z_0 $ $ p_1 $ $ r_1 $ $ x_1 $ $ y_1 $ $ z_1 $ : $ p_{N-1} $ $ r_{N-1} $ $ x_{N-1} $ $ y_{N-1} $ $ z_{N-1} $ [例を見る](https://img.atcoder.jp/toyota-hc-2023spring/d1cb95b8.html?seed=0&output=0+0+0+30+0%0D%0A0+1+360+30+0%0D%0A0+0+715+0+0%0D%0A1+1+0+385+0%0D%0A3+0+30+30+285%0D%0A2+0+0+30+615%0D%0A)

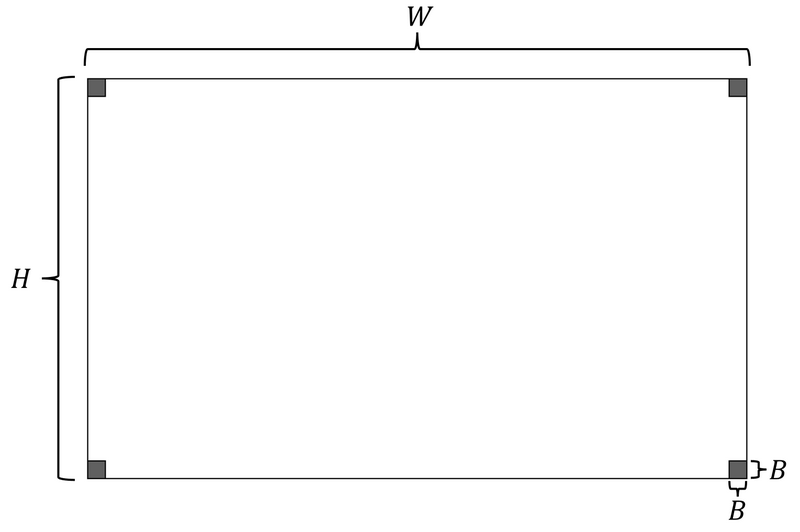
### コンテナの仕様 コンテナは横 $ W $ 、縦 $ H $ 、高さ $ D $ の直方体の四隅に、底面が $ B\times B $ の正方形で高さが $ D $ であるような直方体ブロックが4つ置かれた形状をしている。 下図はコンテナを真上から見た際の形状を示している。  四隅のブロックがある領域には荷物を置くことが出来ず、他の領域に荷物を積み込みたい。 コンテナの高さは $ D $ であるが、今回の問題においては、 $ D $ より高い位置まで荷物を積むことが可能である。ただし、コンテナの高さ $ D $ を越える位置まで積み込む場合、極めて低い評価となる。 ### 荷物の仕様 荷物は全部で $ M $ 種類あり、以下の性質を持つ。 - 荷物は全て直方体であり、 $ i $ 種類目の荷物の大きさは、横 $ w_i $ 、縦 $ h_i $ 、高さ $ d_i $ である。 - $ i $ 種類目の荷物は全部で $ a_i $ 個ある。 - 各荷物は各軸について90度単位で回転可能であるが、一部の種類の荷物は底面を固定した回転しか許されない。 $ i $ 種類目の荷物の回転制限はフラグ $ f_i $ で表され、 $ f_i $ が `Y` の時は自由に回転出来、 $ f_i $ が `N` の時は底面を固定した回転しか出来ない。 - 荷物の種類によって、その上に他の荷物を重ねて置けるかどうかが制限されている。 $ i $ 種類目の荷物の上にものを置くことが許されているかはフラグ $ g_i $ で表され、 $ g_i $ が `Y` の時は上に物を置くことが可能であり、 $ g_i $ が `N` の時は上に物を置いてはならない。ここで、「荷物Aが荷物Bの上に置かれている」とは、荷物Aの底面と荷物Bの上面の共通部分が正の面積を持つことを指す。荷物Bの上部の空間に荷物Aが配置されていても、間に隙間があれば荷物Bの上に置かれているとはみなされない。 ### 荷物の積み込み方 荷物は、真上から垂直に下ろすことで1つずつ積み込んでいく。 このため、荷物を配置する予定位置の上部の空間には他の既に配置した荷物が存在してはならない。 荷物は積み込む前に90度単位で回転可能であるが、荷物の各面がコンテナの側面・底面と平行になるようにしなければならない。 積み込まれた荷物は、底面の面積の $ 6 $ 割(小数点以下切り捨て)以上が、コンテナの底、もしくは他の荷物に接している必要がある。 コンテナの高さ $ D $ を越える位置まで荷物を積み込む場合においても、コンテナの外部や四隅のブロックの上部には荷物を置くことは出来ない。 荷物は任意の順番で積み込むことが出来る(ただし、出来るだけ順番通りに積み込む方が良いスコアが得られる)。 同じ種類の荷物を一度に積み込む必要はなく、種類aの荷物の1つ目→種類bの荷物の1つ目→種類aの荷物の2つ目、のような順番で積み込むことも可能である。 ### 得点 $ i $ 番目に積む荷物の種類を $ p_i $ ( $ 0\leq p_i\leq M-1 $ ) とし、積み込んだ荷物の上面の高さの最大値を $ \mathrm{MaxHeight} $ とする。 この時、以下のペナルティが与えられる。ペナルティは低ければ低いほど良い。 $ (ペナルティ) = 1000 + \mathrm{MaxHeight} + (順番前後ペナルティ) + (収容失敗ペナルティ) $ 順番前後ペナルティは、 $ p $ の転倒数の $ 1000 $ 倍である。すなわち、 $ i < j $ かつ、 $ p_i > p_j $ となるような各 $ (i,j) $ の組に対して、順番前後ペナルティに $ 1000 $ 点が加算される。 収容失敗ペナルティは、 $ \mathrm{MaxHeight}\leq D $ の場合には $ 0 $ であり、そうでない場合には、上面の高さが $ D $ を越えた荷物の体積(超えた部分の体積ではなく、荷物自体の体積)の和を $ E $ としたとき、 $ 1000000 + 1000 E $ となる。 各テストケース毎に、 $ \mathrm{round}(10^9\times \frac{全参加者中の最小ペナルティ}{自身のペナルティ}) $ の**相対評価スコア**が得られ、その和が提出の得点となる。 最終順位はコンテスト終了後に実施されるより多くの入力に対するシステムテストにおける得点で決定される。 暫定テスト、システムテストともに、一部のテストケースで不正な出力や制限時間超過をした場合、そのテストケースの相対評価スコアは0点となり、そのテストケースにおいては「全参加者中の最小ペナルティ」の計算から除外される。 システムテストは **CE 以外の結果を得た一番最後の提出**に対してのみ行われるため、最終的に提出する解答を間違えないよう注意せよ。 #### テストケース数 - 暫定テスト: 50個 - システムテスト: 3000個、コンテスト終了後に [seeds.txt](https://img.atcoder.jp/toyota-hc-2023spring/seeds.txt) (sha256=dfa7c8bc75f309e6c260506e3b354eaf9b7bfb2ef61d1bdaacebc8263c50dd70) を公開 #### 相対評価システムについて 暫定テスト、システムテストともに、CE 以外の結果を得た一番最後の提出のみが順位表に反映される。 相対評価スコアの計算に用いられる各テストケース毎の全参加者中の最小ペナルティの算出においても、順位表に反映されている最終提出のみが用いられる。 順位表に表示されているスコアは相対評価スコアであり、新規提出があるたびに、相対評価スコアが再計算される。 一方、提出一覧から確認出来る各提出のスコアは各テストケース毎のペナルティをそのまま足し合わせたものであり、相対評価スコアは表示されない。 最新以外の提出の、現在の順位表における相対評価スコアを知るためには、再提出が必要である。 不正な出力や制限時間超過をした場合、提出一覧から確認出来るスコアは0となるが、順位表には正解したテストケースに対する相対スコアの和が表示されている。 #### 実行時間について 実行時間には多少のブレが生じます。 また、システムテストでは同時に大量の実行を行うため、暫定テストに比べて数%程度実行時間が伸びる現象が確認されています。 そのため、実行時間制限ギリギリの提出がシステムテストでTLEとなる可能性があります。 プログラム内で時間を計測して処理を打ち切るか、実行時間に余裕を持たせるようお願いします。 ### 入力生成方法 入力は、以下のように生成される。 $ L $ 以上 $ U $ 以下の整数値を一様ランダムに生成する関数を $ \mathrm{rand}(L,U) $ で表す。 - $ D=600 $ とするか $ D=1200 $ とするかをランダムに選択し、コンテナの体積 $ V $ を、4隅のブロック領域を除いた $ V=WHD-4B^2D $ と定義する。 - 2つのパラメータ $ V_{min}, V_{max} $ を $ V_{min}=\mathrm{rand}(\lceil 0.3 V\rceil,\lfloor 0.8 V\rfloor), V_{max}=V_{min}+\lfloor 0.1 V\rfloor $ により決定する。 - 空の荷物の集合から開始し、以下の方法により荷物の体積の合計が $ V_{min} $ 以上となるまで荷物の種類を1つずつ増やしていく。 - 追加する荷物を [荷物候補リスト](https://img.atcoder.jp/toyota-hc-2023spring/d1cb95b8.csv) からランダムに選択する(既に選ばれたものが再度選ばれる可能性もある)。 - 追加する荷物の個数 $ a_i $ を決定する。個数の決定方法は、荷物の体積に依存する。 - 体積が $ 5\times 10^7 $ 以上の場合、 $ a_i=1 $ 。 - 体積が $ 5\times 10^7 $ 未満 $ 10^7 $ 以上の場合、 $ a_i $ は $ 1 $ ～ $ 3 $ 個の間で、下記の方法でランダムに決定される。 - 体積が $ 10^7 $ 未満 $ 2.5\times 10^6 $ 以上の場合、 $ a_i $ は $ 1 $ ～ $ 10 $ 個の間で、下記の方法でランダムに決定される。 - 体積が $ 2.5\times 10^6 $ 未満の場合、 $ a_i $ は $ 1 $ ～ $ 30 $ 個の間で、下記の方法でランダムに決定される。 - 荷物の個数をランダムに決定する際、個数 $ a $ が選ばれる確率は $ a^{-2} $ に比例する。たとえば $ 1 $ ～ $ 3 $ の中から $ 2 $ が選ばれる確率は $ 2^{-2}/(1^{-2}+2^{-2}+3^{-2}) $ である。 - 荷物の体積の合計が $ V_{min} $ 以上となって処理が終了した際、体積の合計が $ V_{max} $ より大きければ、荷物の集合を空に戻して荷物の集合を作る処理をやり直す。 - 実数 $ F $ を $ 0 $ 以上 $ 0.3 $ 未満の実数の間でランダムに生成する。各荷物 $ i $ について確率 $ F $ で $ f_i $ を `N` とし、それ以外の場合 `Y` とする。 - 各荷物 $ i $ について $ g_i $ を `Y` と初期化し、以下の処理を繰り返すことで $ g $ を変化させる。 - 50% の確率で、 $ g $ を変化させる処理を終了する。 - $ g_i $ = `Y` であるランダムな荷物 $ i $ を選ぶ。ない場合は終了する。 - $ g_i $ を `N` に変化させる。ただし、 $ g_i $ が `N` となっている荷物の底面積の和が、コンテナの底面積 $ WH-4B^2 $ の $ 6 $ 割より大きくなった場合、 $ g_i $ を`Y` に戻し、 $ g $ を変化させる処理を終了する。 ### ツール(入力ジェネレータ・ビジュアライザ) - [Web版](https://img.atcoder.jp/toyota-hc-2023spring/d1cb95b8.html): ローカル版より高性能でアニメーション表示が可能です。 - [ローカル版](https://img.atcoder.jp/toyota-hc-2023spring/d1cb95b8_v2.zip): 使用するには[Rust言語](https://www.rust-lang.org/ja)のコンパイル環境をご用意下さい。入力生成プログラムの実装に誤りがあったため、修正版に差し替えました。再ダウンロードをお願いします。 - [Windows用のコンパイル済みバイナリ](https://img.atcoder.jp/toyota-hc-2023spring/d1cb95b8_windows_v2.zip): Rust言語の環境構築が面倒な方は代わりにこちらをご利用下さい。 コンテスト期間中に、任意のseedに対する(公式・自作)ビジュアライザの出力画像・動画共有及び解法・考察に関する言及が可能です。 必須ではありませんが、[Twitterのハッシュタグ #TOYOTAHC2023SPRING](https://twitter.com/search?q=%23TOYOTAHC2023SPRING&src=typed_query&f=live)をご利用下さい。