AT_ttpc2023_e R-Connected Components

正整数 $ R $ に対し、以下の無限無向グラフの連結成分数を $ f(R) $ と定義します。 - 頂点集合は $ \mathbb Z^2 $ である。すなわち、任意の $ 2 $ つの整数 $ x, y $ に対し、頂点 $ (x, y) $ が存在する。 - 頂点 $ (x_1, y_1) $ と頂点 $ (x_2, y_2) $ の間には、 $ |x_1 - x_2|^2 + |y_1 - y_2|^2 = R $ であるとき、かつそのときに限り辺が存在する。 正整数 $ R $ が与えられるので、 $ f(R) $ を出力してください。ただし、 $ f(R) $ が有限でないときは、`inf` を出力してください。 $ T $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。

入力は以下の形式で標準入力から与えられる。 > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ $ \mathrm{case}_i $ は $ i $ 個目のテストケースを表す。各テストケースは以下の形式で与えられる。 > $ R $

各テストケースについて、 $ f(R) $ が有限ならば $ f(R) $ を、 $ f(R) $ が有限でないならば `inf` を出力せよ。

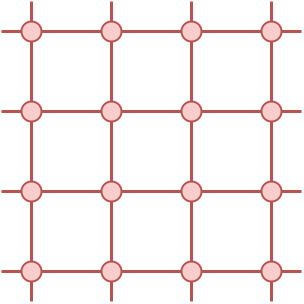
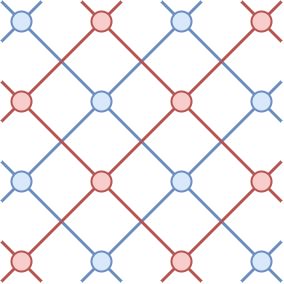
### 部分点 - 追加の制約 $ R \le 10^3 $ を満たすデータセットに正解した場合は $ 25 $ 点が与えられる。 ### Sample Explanation 1 $ 1 $ 個目のテストケースでは、 $ R=1 $ です。以下のように辺が張られるので、連結成分の個数は $ 1 $ 個です。  $ 2 $ 個目のテストケースでは、 $ R=2 $ です。以下のように辺が張られるので、連結成分の個数は $ 2 $ 個です。  $ 3 $ 個目のテストケースでは、 $ R=3 $ です。このグラフには辺がなく、連結成分の個数は有限ではありません。 ### Constraints - $ 1 \le T \le 100 $ - $ 1 \le R \le 10^9 $ - 入力はすべて整数