AT_ttpc2023_e R-Connected Components

对于正整数 $R$，定义如下无限无向图的连通分量数为 $f(R)$。 - 顶点集合为 $\mathbb{Z}^2$，即对于任意两个整数 $x, y$，都存在顶点 $(x, y)$。 - 当且仅当 $|x_1 - x_2|^2 + |y_1 - y_2|^2 = R$ 时，顶点 $(x_1, y_1)$ 与顶点 $(x_2, y_2)$ 之间有一条边。 给定正整数 $R$，请输出 $f(R)$。如果 $f(R)$ 不是有限的，则输出 `inf`。 有 $T$ 组测试数据，请分别输出每组的答案。

输入从标准输入读入，格式如下： > $T\ \mathrm{case}_1\ \mathrm{case}_2\ \vdots\ \mathrm{case}_T$ $\mathrm{case}_i$ 表示第 $i$ 组测试数据，每组格式如下： > $R$

对于每组测试数据，如果 $f(R)$ 有限，则输出 $f(R)$，否则输出 `inf`。

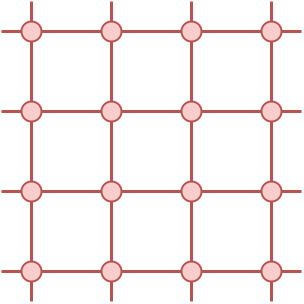
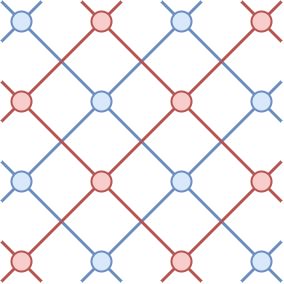
## 部分分 - 对于满足额外约束 $R \le 10^3$ 的数据集，得分为 $25$ 分。 ## 样例解释 1 第 $1$ 个测试点为 $R=1$。如图所示，边的连接方式使得连通分量个数为 $1$。  第 $2$ 个测试点为 $R=2$。如图所示，边的连接方式使得连通分量个数为 $2$。  第 $3$ 个测试点为 $R=3$。该图中没有边，因此连通分量个数不是有限的。 # 数据范围 - $1 \le T \le 100$ - $1 \le R \le 10^9$ - 输入均为整数。 由 ChatGPT 5 翻译