AT_ttpc2023_k Dense Planting

给定一个整数 $K$，请构造一个无向图，使其满足以下条件，并且边的数量尽可能少。 - 顶点数 $N$ 满足 $1 \le N \le 100$。 - 边数 $M$ 满足 $M \le 10^5$。 - 当所有的边都互相区分时，图中恰好存在 $K$ 个不同的生成树。也就是说，从 $M$ 条边中选择若干条边的方法共有 $2^M$ 种，其中恰好有 $K$ 种选择能够使剩下的边组成一棵树。

输入通过标准输入按如下格式给出。 > $K$

输出满足条件的无向图，要求按如下格式输出。若存在多个满足条件的图，输出其中任意一个均可。 > $N$ $M$ > $U_1$ $V_1$ > $\vdots$ > $U_M$ $V_M$ 其中 $U_i, V_i\ (1 \le i \le M)$ 表示第 $i$ 条边连接了顶点 $U_i$ 和顶点 $V_i$。

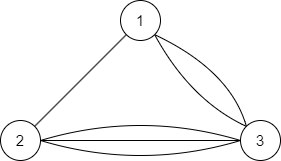
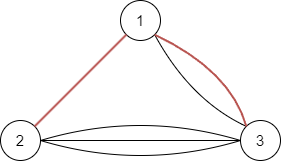
### 得分 当程序对所有测试用例均输出满足题意要求时，该提交将被判定为 AC。此时，所有测试点中 $M$ 的最大值为 $M_{\max}$，评分标准如下： 条件 得分 $10^4 < M_{\max} \le 10^5$ 20分 $10^3 < M_{\max} \le 10^4$ 60分 $M_{\max} \le 10^3$ 100分 ### 样例解释 1 输出的图如下图所示：  例如，选择下述 $2$ 条边就可以构成该图的一棵生成树：  - 由边 $1 - 2$ 和边 $1 - 3$ 构成的生成树有 $2$ 种。 - 由边 $1 - 2$ 和边 $2 - 3$ 构成的生成树有 $3$ 种。 - 由边 $1 - 3$ 和边 $2 - 3$ 构成的生成树有 $6$ 种。 因此，总共存在 $11$ 个生成树。 另外，以下这样的图同样存在 $11$ 个生成树，因此，下述输出同样视为正确。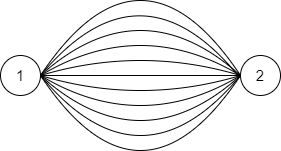  ``` 2 11 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ``` ### 数据范围 - $K$ 是整数。 - $1 \le K \le 10^9$。 由 ChatGPT 5 翻译