AT_ttpc2023_k Dense Planting

整数 $ K $ が与えられます。以下の条件を満たすできるだけ辺の少ない無向グラフを $ 1 $ つ構築してください。 - 頂点の数 $ N $ は $ 1 $ 以上 $ 100 $ 以下 - 辺の数 $ M $ は $ 10^5 $ 以下 - 辺はすべて区別できるものとしたとき、グラフの全域木がちょうど $ K $ 個存在する。すなわち、 $ M $ 本の辺からいくつかの辺を選ぶ方法 $ 2^M $ 通りのうち、それら以外の辺を削除するとグラフが木になるようなものがちょうど $ K $ 通り存在する。

入力は以下の形式で標準入力から与えられる。 > $ K $

条件を満たす無向グラフを以下の形式で出力せよ。条件を満たすグラフが複数ある場合、そのいずれを出力してもよい。 > $ N $ $ M $ $ U_1 $ $ V_1 $ $ \vdots $ $ U_M $ $ V_M $ $ U_i, V_i\ (1 \le i \le M) $ は $ i $ 本目の辺が頂点 $ U_i $ と頂点 $ V_i $ を結ぶことを表す。

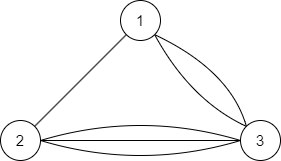
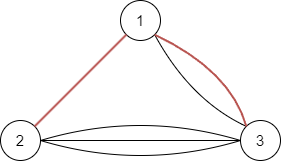
### 得点 プログラムがすべてのテストケースで問題文の条件を満たす出力を行ったとき、その提出は AC となる。このとき、すべてのテストケースにおける $ M $ の最大値を $ M_{\max} $ として以下の点数が与えられる。 条件 点数 $ 10^4 < M_{\max} \le 10^5 $ $ 20 $ 点 $ 10^3 < M_{\max} \le 10^4 $ $ 60 $ 点 $ M_{\max} \le 10^3 $ $ 100 $ 点 ### Sample Explanation 1 出力のグラフは以下の図で表されます。  例えば、以下の $ 2 $ 辺を選ぶとこのグラフの全域木になります。  - 辺 $ 1 - 2 $ と辺 $ 1 - 3 $ からなる全域木が $ 2 $ 通り - 辺 $ 1 - 2 $ と辺 $ 2 - 3 $ からなる全域木が $ 3 $ 通り - 辺 $ 1 - 3 $ と辺 $ 2 - 3 $ からなる全域木が $ 6 $ 通り あるので、全部で $ 11 $ 個の全域木が存在します。 また、以下のようなグラフにも全域木が $ 11 $ 個存在するため、次の出力も正解とみなされます。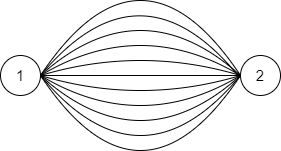  ``` 2 11 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ``` ### Constraints - $ K $ は整数 - $ 1 \le K \le 10^9 $