AT_ttpc2023_o 2D Parentheses

$ 2 $ 次元平面上に開きカッコと閉じカッコがそれぞれ $ N $ 個ずつあります。 $ i $ 番目の開きカッコの座標は $ (x_{1, i}, y_{1, i}) $ 、 $ i $ 番目の閉じカッコの座標は $ (x_{2, i}, y_{2, i}) $ です。 $ x_{1, i} < x_{2, j} $ かつ $ y_{1, i} < y_{2, j} $ であるときに限り、 $ i $ 番目の開きカッコと $ j $ 番目の閉じカッコを平面上から削除し、代わりに $ 4 $ 点 $ (x_{1, i}, y_{1, i}), (x_{1, i}, y_{2, j}), (x_{2, j}, y_{2, j}), (x_{2, j}, y_{1, i}) $ を頂点とする長方形を平面に配置することができます。 任意の異なる $ 2 $ つの長方形の共通部分が、面積が $ 0 $ となるか、または一方の長方形に一致するように $ N $ 個の長方形を平面に配置することができるかを判定し、できるならばそのような配置の方法を $ 1 $ つ求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ x_{1, 1} $ $ y_{1, 1} $ $ x_{1, 2} $ $ y_{1, 2} $ $ \vdots $ $ x_{1, N} $ $ y_{1, N} $ $ x_{2, 1} $ $ y_{2, 1} $ $ x_{2, 2} $ $ y_{2, 2} $ $ \vdots $ $ x_{2, N} $ $ y_{2, N} $

条件を満たす配置が存在しない場合、`No` と一行に出力せよ。 条件を満たす配置が存在する場合、まず `Yes` と一行に出力せよ。その後、そのような配置において $ i $ 番目 $ (1 \le i \le N) $ の開きカッコに $ c_i $ 番目 $ (1 \le c_i \le N) $ の閉じカッコが対応するとして、 $ i $ 行目に $ c_i $ を出力せよ。 条件を満たす配置が複数存在する場合は、そのうちのどれを出力しても正解となる。

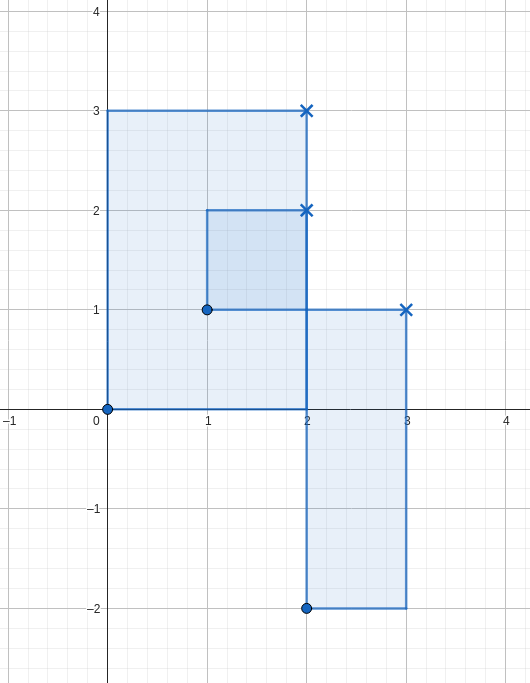
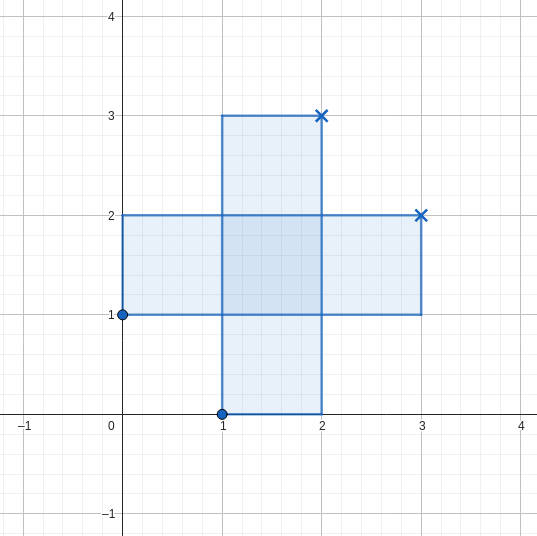
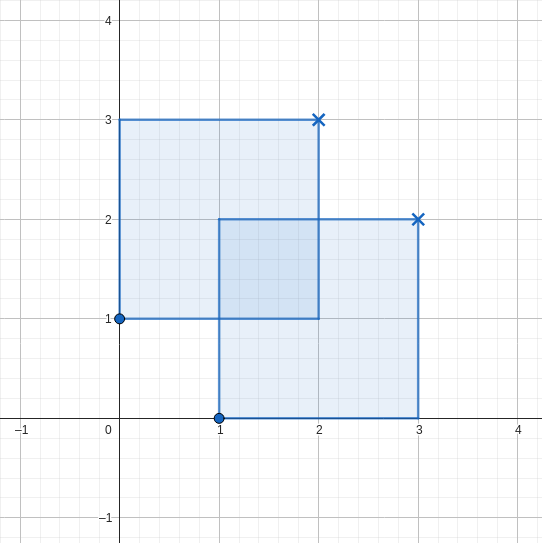
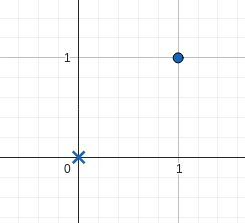
### Sample Explanation 1 下図のように長方形を配置すると、条件を満たします。 ただし、図において、丸は開きカッコ、バツ印は閉じカッコを表します。  ### Sample Explanation 2 図のように、どのように長方形を配置しても、条件を満たすことができません。   ### Sample Explanation 3 残念ながら、そもそも長方形を配置することができません。  ### Constraints - $ 1 \leq N \leq 2 \times 10^5 $ - $ -10^9 \leq x_{p, i}, y_{p, i} \leq 10^9 $ - $ (p, i) \neq (q, j) $ ならば $ (x_{p, i}, y_{p, i}) \neq (x_{q, j}, y_{q, j}) $ - 入力は全て整数