AT_ttpc2023_o 2D Parentheses

在 $2$ 维平面上有 $N$ 个左括号和 $N$ 个右括号。第 $i$ 个左括号的坐标为 $(x_{1, i}, y_{1, i})$，第 $i$ 个右括号的坐标为 $(x_{2, i}, y_{2, i})$。 只有当 $x_{1, i} < x_{2, j}$ 且 $y_{1, i} < y_{2, j}$ 时，才能将第 $i$ 个左括号和第 $j$ 个右括号从平面上删除，并在平面上放置以 $4$ 个点 $(x_{1, i}, y_{1, i})$、$(x_{1, i}, y_{2, j})$、$(x_{2, j}, y_{2, j})$、$(x_{2, j}, y_{1, i})$ 为顶点的矩形。 请判断是否存在一种方法，在平面上放置 $N$ 个矩形，使得任意两个不同的矩形的公共部分要么面积为 $0$，要么其中一个矩形完全包含于另一个矩形之中。如果存在，给出其中一种矩形的匹配方式。

输入以如下形式从标准输入读入。 > $N$ > $x_{1, 1}\ y_{1, 1}$ > $x_{1, 2}\ y_{1, 2}$ > $\vdots$ > $x_{1, N}\ y_{1, N}$ > $x_{2, 1}\ y_{2, 1}$ > $x_{2, 2}\ y_{2, 2}$ > $\vdots$ > $x_{2, N}\ y_{2, N}$

如果不存在满足条件的放置方式，请输出一行 `No`。 如果存在满足条件的放置方式，第一行输出 `Yes`。接下来输出 $N$ 行，第 $i$ 行输出 $c_i$，表示第 $i$ 个左括号与第 $c_i$ 个右括号配对。 如果存在多种满足条件的放置方式，输出其中任意一种即可。

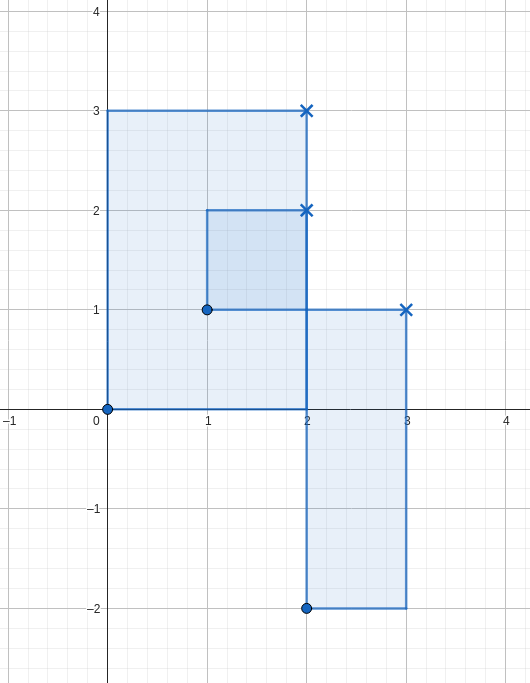
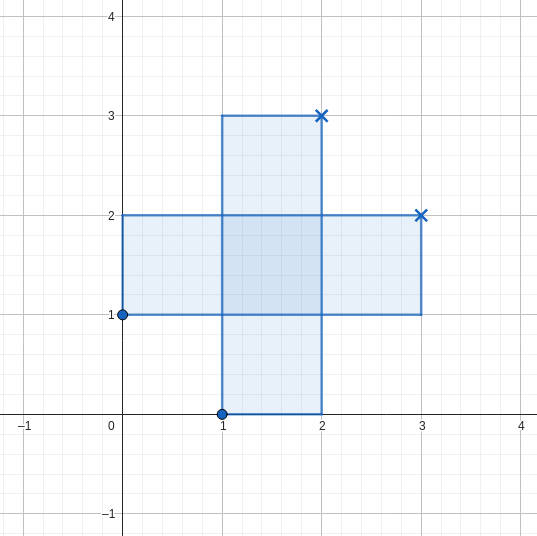
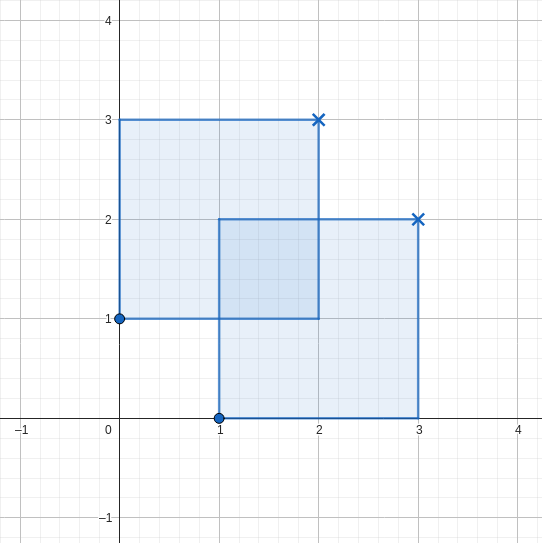
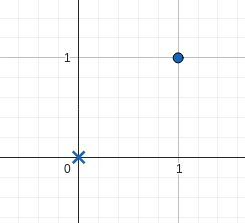
### 样例解释 1 如图所示，可以按照下图放置矩形，满足条件。 其中，图中的圆圈表示左括号，叉表示右括号。  ### 样例解释 2 如图所示，无论如何放置矩形，都无法满足条件。   ### 样例解释 3 遗憾的是，无法放置任何矩形。  ### 约束条件 - $1 \leq N \leq 2 \times 10^5$ - $-10^9 \leq x_{p, i}, y_{p, i} \leq 10^9$ - 若 $(p, i) \neq (q, j)$，则 $(x_{p, i}, y_{p, i}) \neq (x_{q, j}, y_{q, j})$。 - 所有输入均为整数。 由 ChatGPT 5 翻译