AT_ttpc2023_p Bridge Elimination

有一个 $N$ 个顶点的无向图。这些顶点从 $1$ 到 $N$ 编号，每个顶点 $i\ (1 \le i \le N)$ 上写有一个整数 $A_i$。该图初始没有边，你可以自由地添加边。 对于该图而言，使其成为一个简单图的连边方式共有 $2^{\frac{N(N-1)}{2}}$ 种。对于每一种方式，计算如下的 **得分**，并求所有可能连边方式下得分的总和，对 $998244353$ 取模后输出。 - 如果图不连通，则该方案的 **得分** 为 $0$。 - 如果图连通，将该图中的所有桥边删除，得到图 $G$。对 $G$ 的每个连通分量，计算其所有顶点对应 $A_i$ 的和；将这些和相乘，作为该方案的 **得分**。

输入从标准输入给出，格式如下： > $N$ $A_1$ $A_2$ $\dots$ $A_N$

请输出答案。

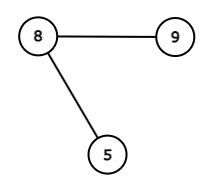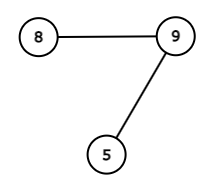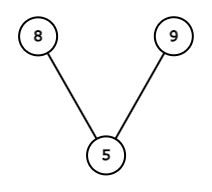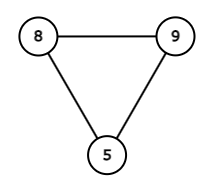
## 样例解释 1 对于 $3$ 个顶点的简单连通无向图，共有如下 $4$ 种情况。     四种情况下得分从左到右分别为 $360, 360, 360, 22$，所以答案为 $1102$。 ## 样例解释 3 请将答案对 $998244353$ 取模后输出。 ## 数据范围 - $1 \le N \le 400$ - $0 \le A_i < 998244353\ (1 \le i \le N)$ - 输入均为整数。 由 ChatGPT 5 翻译