AT_ttpc2023_p Bridge Elimination

$ N $ 頂点の無向グラフがあります。このグラフの頂点には $ 1 $ から $ N $ までの番号がつけられており、頂点 $ i\ (1 \le i \le N) $ には整数 $ A_i $ が書かれています。このグラフには辺がありませんが、あなたが自由に辺を張ることができます。 このグラフが単純グラフとなるような辺の張り方は $ 2^{\frac{N(N-1)}{2}} $ 通り存在しますが、そのすべてについて以下の **スコア** を計算し、その総和を $ 998244353 $ で割った余りを求めてください。 - グラフが連結でないとき、その **スコア** は $ 0 $ である。 - グラフが連結なとき、グラフから橋である辺を取り除いたグラフを $ G $ とする。 $ G $ の各連結成分について頂点に書かれた整数の和を考え、その総積を **スコア** とする。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A_1 $ $ A_2 $ $ \dots $ $ A_N $

答えを出力せよ。

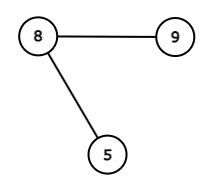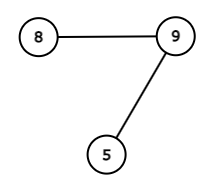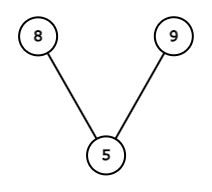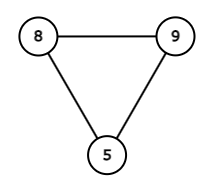
### Sample Explanation 1 $ 3 $ 頂点の単純連結無向グラフは、次の $ 4 $ 通りです。     スコアは左からそれぞれ $ 360, 360, 360, 22 $ なので、答えは $ 1102 $ です。 ### Sample Explanation 3 答えを $ 998244353 $ で割った余りを出力してください。 ### Constraints - $ 1 \le N \le 400 $ - $ 0 \le A_i \lt 998244353\ (1 \le i \le N) $ - 入力はすべて整数