AT_ttpc2024_1_a Don't Detect Cycle
题目描述
有一个图 $G$,由 $N$ 个顶点组成,顶点编号为 $1, 2, \ldots, N$。起初,图中没有任何边。
接下来,我们将向图中添加 $M$ 条无向边。图中最终的边是预先确定的:第 $i$ 条边 $(1 \le i \le M)$ 连接顶点 $u_i$ 和 $v_i$。我们称其为边 $i$。添加后的图确保是简单图。
现在,你要判断是否存在一种排列 $(P_1, P_2, \ldots, P_M)$ 满足以下条件,并如满足条件则给出这样的一个实例。
**条件**:
- 按照索引顺序为 $i = 1, 2, \ldots, M$,依次执行以下操作:
1. 如果当前图中包含 $u_{P_i}$ 或 $v_{P_i}$ 的环存在,则立即停止操作,此时条件不成立。
2. 在图中添加边 $P_i$(即连接顶点 $u_{P_i}$ 和 $v_{P_i}$ 的无向边)。
共给出 $T$ 个测试用例,请分别解决每个测试用例。
**环的定义**:图 $G$ 中的环是指满足以下条件的顶点序列 $(v_0, \dots, v_{L-1})$ 和边序列 $(e_0, \dots, e_{L-1})$:
- $L \ge 1$
- 若 $i \neq j$,则 $v_i \neq v_j$ 且 $e_i \neq e_j$
- 对于 $0 \le i \le L-2$,边 $e_i$ 连接顶点 $v_i$ 和 $v_{i+1}$
- 边 $e_{L-1}$ 连接顶点 $v_{L-1}$ 和 $v_0$
**简单图的定义**:图 $G$ 被称作简单图,是因为没有自环和多重边。
输入格式
输入通过标准输入给出,格式如下:
> $T$
> $\text{case}_1$
> $\text{case}_2$
> $\vdots$
> $\text{case}_T$
每个 $\text{case}_i (1 \le i \le T)$ 对应一个测试用例,格式如下:
> $N$ $M$
> $u_1$ $v_1$
> $u_2$ $v_2$
> $\vdots$
> $u_M$ $v_M$
输出格式
对于每个测试用例,如果存在满足条件的排列 $(P_1, P_2, \ldots, P_M)$,则输出这样一个排列,元素之间用空格隔开;如果不存在,则输出 `-1`。
说明/提示
- 输入中所有的数值均为整数。
- $1 \le T \le 2000$
- 每个测试用例满足:
- $2 \le N \le 4000$
- $1 \le M \le 4000$
- $1 \le u_i, v_i \le N$ ($1 \le i \le M$)
- 添加所有给定的边后,图为简单图。
- 每份输入文件中,所有测试用例 $N, M$ 总和不超过 $4000$。
**部分评分**
若仅回答满足以下条件的数据集,可获得 $30$ 分:
- $T \le 50$
- 每个测试用例满足:
- $N \le 100$
- $M \le 100$
- 每份输入文件中,所有测试用例 $N, M$ 总和不超过 $100$
### 示例说明 1
给定图如下图所示:
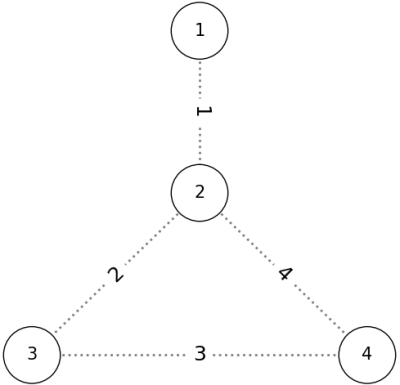
按顺序 $P = (1, 2, 3, 4)$ 添加边后,图为如下图、符合条件:
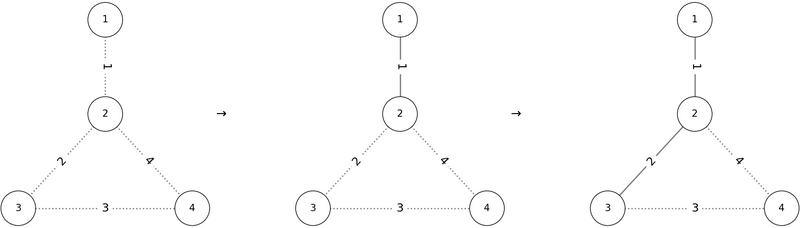
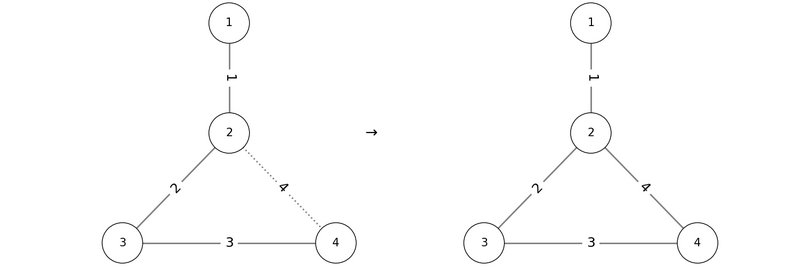
因此,`1 2 3 4` 是一个正确的输出方案。若按顺序 $P = (2, 3, 4, 1)$ 添加边,则在添加边 $1$ 时会形成包含顶点 $2$ 的环,故不满足条件:
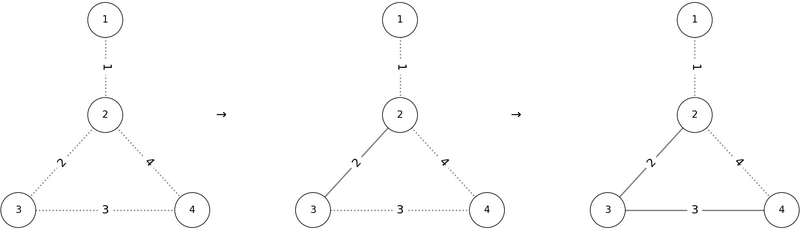
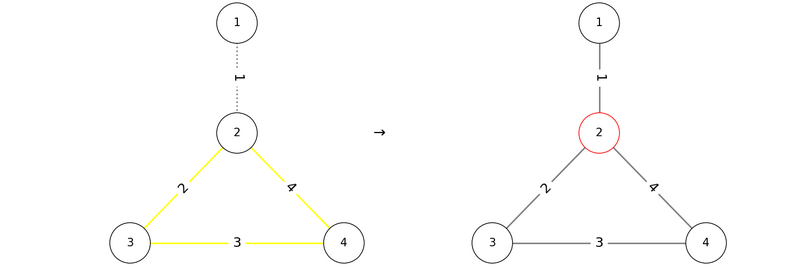
另外,像 $P = (1, 4, 3, 2)$ 或 $P = (2, 4, 1, 3)$ 的排列也符合条件。
### 示例说明 2
如果不存在满足条件的排列 $P$,则请输出 `-1`。注意,图不一定连通。
**本翻译由 AI 自动生成**