AT_ttpc2024_1_a Don't Detect Cycle

You are given a graph $ G $ consisting of $ N $ vertices numbered $ 1, 2, \ldots, N $ . Initially, $ G $ has no edges. You will add $ M $ undirected edges to $ G $ . The final shape of the graph is predetermined, and the $ i $ -th edge to be added $ (1 > You must be able to add all $ M $ edges to $ G $ by following this procedure: > > - For $ i = 1, 2, \dots, M $ , repeat the following: > 1. If there is already a cycle in $ G $ containing either vertex $ u_{P_i} $ or vertex $ v_{P_i} $ , the condition is not satisfied, and the procedure ends. > 2. Add edge $ P_i $ (the undirected edge connecting $ u_{P_i} $ and $ v_{P_i} $ ) to $ G $ . You are given $ T $ test cases; solve each of them. What is a cycle? A cycle in $ G $ is defined as a sequence of vertices $ (v_0, \dots, v_{L - 1}) $ and a sequence of edges $ (e_0, \dots, e_{L - 1}) $ that satisfy the following conditions: - $ L \ge 1 $ - $ i \neq j \implies v_i \neq v_j, e_i \neq e_j $ - For $ 0 \le i \le L - 2 $ , edge $ e_i $ connects vertices $ v_i $ and $ v_{i+1} $ - Edge $ e_{L-1} $ connects vertices $ v_{L-1} $ and $ v_0 $ What does it mean for a graph to be simple? A graph $ G $ is simple if it contains no self-loops or multiple edges.

The input is given from Standard Input in the following format: > $ T $ $ \text{case}_1 $ $ \text{case}_2 $ $ \vdots $ $ \text{case}_T $ Here, $ \text{case}_i\ (1

For each test case, if a permutation $ (P_1, P_2, \ldots, P_M) $ satisfying the conditions exists, output such a $ P $ separated by spaces. If no such permutation exists, output `-1`.

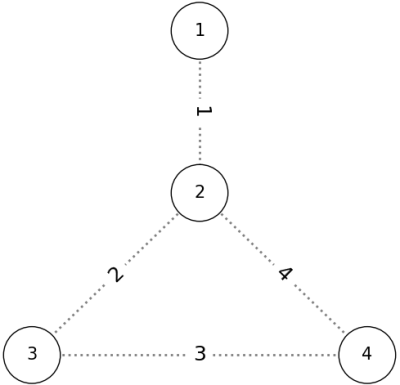
### Subtasks $ 30 $ points will be awarded for passing the test set satisfying: - $ T \le 50 $ - For each test case: - $ N \le 100 $ - $ M \le 100 $ - The sum of $ N $ over all test cases is at most $ 100 $ . - The sum of $ M $ over all test cases is at most $ 100 $ . 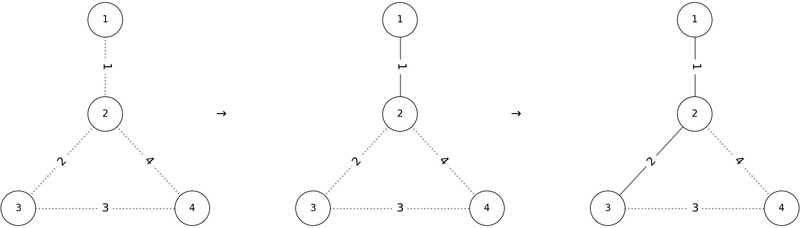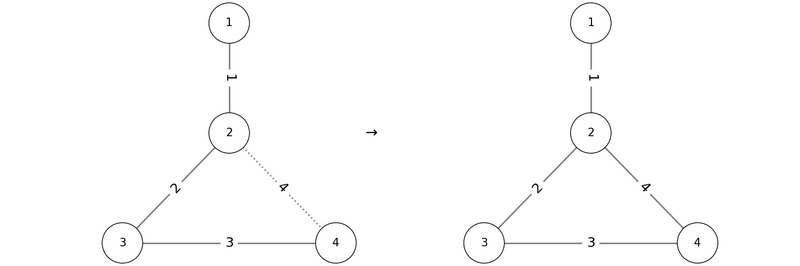### Sample Explanation 1 The given graph has the following shape:  If we add the edges in the order $ P = (1, 2, 3, 4) $ , the conditions are satisfied as shown below:   Thus, `1 2 3 4` is one valid output. However, if we add edges in the order $ P = (2, 3, 4, 1) $ , a cycle containing vertex $ 2 $ is created before edge $ 1 $ can be added, so the conditions are not satisfied.   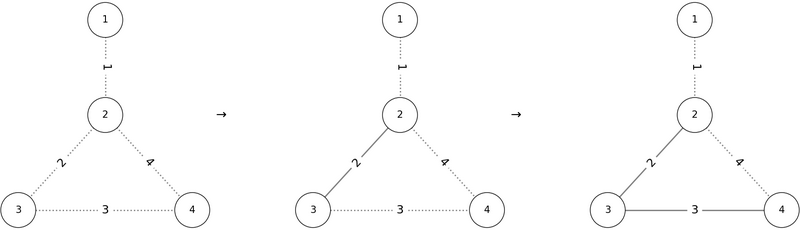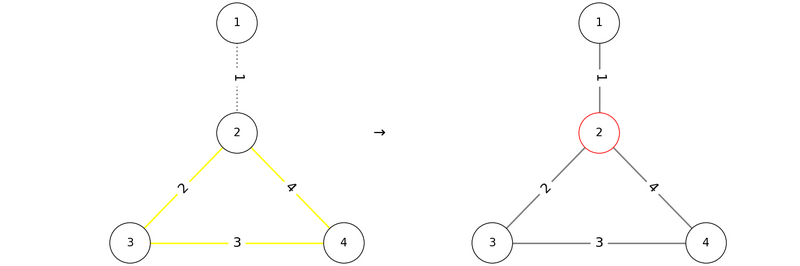Other valid outputs include $ P = (1, 4, 3, 2) $ or $ P = (2, 4, 1, 3) $ . ### Sample Explanation 2 If no valid $ P $ exists, output `-1`. Note that the graph is not necessarily connected. ### Constraints - All input values are integers. - $ 1 \le T \le 2000 $ - For each test case: - $ 2 \le N \le 4000 $ - $ 1 \le M \le 4000 $ - $ 1 \le u_i, v_i \le N\ (1