AT_ttpc2024_1_a Don't Detect Cycle

$ N $ 頂点からなるグラフ $ G $ があり、頂点には $ 1, 2, \ldots, N $ の番号がついています。はじめ、 $ G $ には辺がありません。 これから、 $ G $ に $ M $ 本の無向辺を追加します。追加後のグラフの形は決まっており、追加する辺のうち $ i $ 番目の辺 $ (1 > 以下の手順を行って、 $ G $ に $ M $ 本の辺をすべて追加することができる。 > > - $ i = 1, 2, \dots, M $ の順に以下を繰り返す: > 1. $ G $ に頂点 $ u_{P_i} $ または頂点 $ v_{P_i} $ を含むサイクルが存在するとき、条件は満たされないものとして手順を終了する。 > 2. $ G $ に辺 $ P_i $ （頂点 $ u_{P_i} $ と頂点 $ v_{P_i} $ を結ぶ無向辺）を追加する。 $ T $ 個のテストケースが与えられるので、それぞれについて解いて下さい。 サイクルとは？ $ G $ におけるサイクルとは、頂点の列 $ (v_0, \dots, v_{L - 1}) $ と 辺の列 $ (e_0, \dots, e_{L - 1}) $ であって以下の条件を満たすもののことを言います。 - $ L \ge 1 $ - $ i \neq j \implies v_i \neq v_j, e_i \neq e_j $ - $ 0 \le i \le L - 2 $ に対して、辺 $ e_i $ は頂点 $ v_i $ と頂点 $ v_{i+1} $ を結ぶ - 辺 $ e_{L-1} $ は頂点 $ v_{L-1} $ と頂点 $ v_0 $ を結ぶ グラフが単純とは？ グラフ $ G $ が単純であるとは、 $ G $ が自己ループ及び多重辺を含まない事を言います。

入力は以下の形式で標準入力から与えられる。 > $ T $ $ \text{case}_1 $ $ \text{case}_2 $ $ \vdots $ $ \text{case}_T $ ここで、 $ \text{case}_i\ (1

各テストケースについて、条件を満たす順列 $ (P_1, P_2, \ldots, P_M) $ が存在する場合は、そのような $ P $ を空白区切りで出力せよ。存在しない場合は、`-1` を出力せよ。

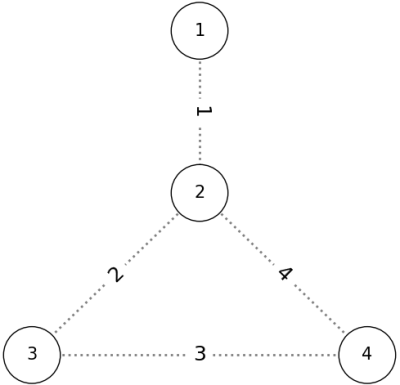
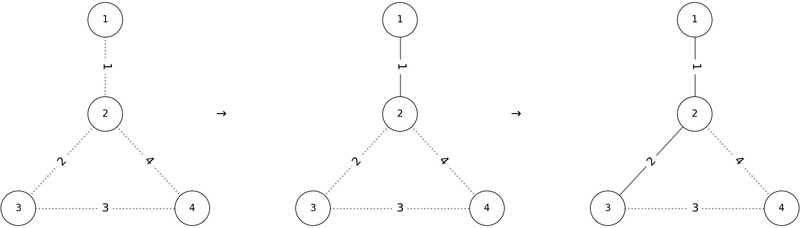
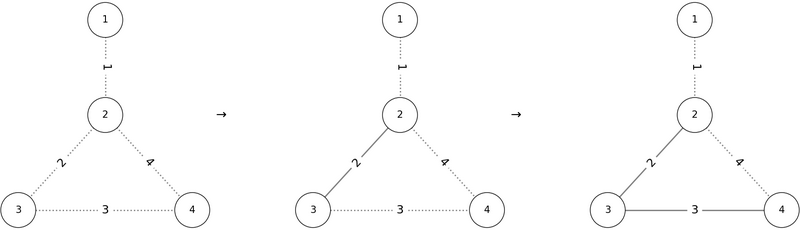
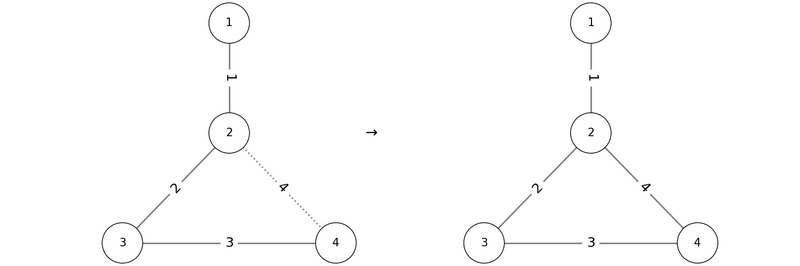
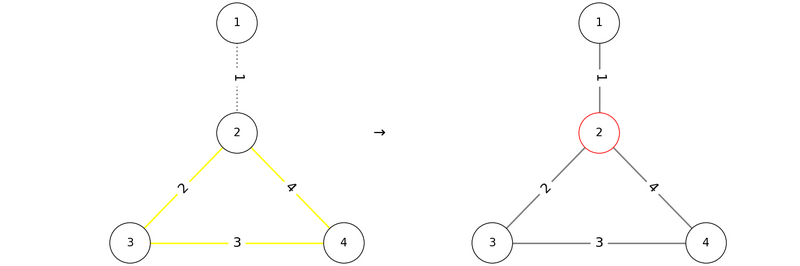
### 部分点 以下の制約を満たすデータセットに正解した場合は $ 30 $ 点が与えられる。 - $ T \le 50 $ - 各テストケースについて: - $ N \le 100 $ - $ M \le 100 $ - 各入力ファイルについて、 $ N $ , $ M $ の総和はそれぞれ $ 100 $ を超えない ### Sample Explanation 1 与えられたグラフは以下の図のような形をしています。  これに対し、 $ P = (1, 2, 3, 4) $ の順で辺を追加すると、以下の図のように条件を満たします。   したがって、`1 2 3 4` は正しい出力の $ 1 $ つです。 しかし、 $ P = (2, 3, 4, 1) $ の順で辺を追加すると、辺 $ 1 $ を追加する際に頂点 $ 2 $ を含むサイクルが存在するため、条件を満たしません。   他にも、 $ P = (1, 4, 3, 2) $ や $ P = (2, 4, 1, 3) $ などが条件を満たします。 ### Sample Explanation 2 条件を満たす $ P $ が存在しない場合、`-1` を出力して下さい。また、グラフは連結とは限らないことに注意してください。 ### Constraints - 入力はすべて整数 - $ 1 \le T \le 2000 $ - 各テストケースについて: - $ 2 \le N \le 4000 $ - $ 1 \le M \le 4000 $ - $ 1 \le u_i, v_i \le N\ (1