AT_ttpc2024_1_c Segment Tree

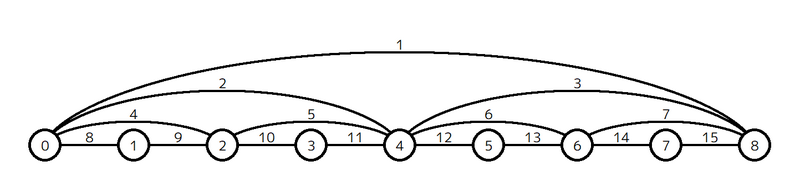
给你一个无向图 $G$，它包含 $2^N + 1$ 个顶点和 $2^{N+1} - 1$ 条边。顶点的编号分别是 $0, 1, \dots, 2^N$，边的编号为 $1, 2, \dots, 2^{N+1}-1$。 图中的边分为 $N+1$ 种类型，从类型 $0$ 到类型 $N$。第 $i$ 种类型（$0 \le i \le N$）的边总共有 $2^i$ 条，编号依次为 $2^i + 0, 2^i + 1, \dots, 2^i + (2^i - 1)$。编号为 $2^i + j$ 的边（$0 \le j \le 2^i - 1$）连接顶点 $j \times 2^{N-i}$ 和顶点 $(j + 1) \times 2^{N-i}$，边的长度为 $C_{2^i + j}$。 例如，当 $N = 3$ 时，图 $G$ 如下图所示。  你需要处理 $Q$ 个查询，查询分为两种类型： - `1 j x`：将编号为 $j$ 的边的长度更新为 $x$。 - `2 s t`：询问从顶点 $s$ 到顶点 $t$ 的最短路径长度。

输入包括以下内容。注意，顶点编号从 $0$ 开始，而边的编号从 $1$ 开始。 > $N$ $C_1$ $C_2$ $\cdots$ $C_{2^{N+1}-1}$ $Q$ $\text{query}_1$ $\text{query}_2$ $\vdots$ $\text{query}_Q$ 每个 $\text{query}_i$ 表示第 $i$ 个查询，查询有以下两种格式之一： > 1 $j$ $x$ > 2 $s$ $t$

对于每一个 `2 s t` 类型的查询，输出一行答案，共计 $m$ 行，其中 $m$ 是 `2 s t` 查询的数量。第 $i$ 行对应第 $i$ 个 `2 s t` 查询的结果。

- 输入的所有数值均为整数。 - $1 \le N \le 18$ - $1 \le C_j \le 10^7$，$ (1\le j\le 2^{N+1}-1$） - $1 \le Q \le 2 \times 10^5$ - 对于 `1 j x` 类型的查询，$1 \le j \le 2^{N+1}-1$ 且 $1 \le x \le 10^7$ - 对于 `2 s t` 类型的查询，$0 \le s < t \le 2^N$ - 至少存在一个 `2 s t` 类型的查询 ### 部分得分 如果在不包含 `1 j x` 类型查询的数据集上正确解答，可以获得 $30$ 分。 **本翻译由 AI 自动生成**