AT_ttpc2024_1_c Segment Tree

You are given an undirected graph $ G $ with $ 2^N + 1 $ vertices and $ 2^{N+1} - 1 $ edges. The vertices are numbered $ 0, 1, \dots, 2^N $ , and the edges are numbered $ 1, 2, \dots, 2^{N+1}-1 $ . Each edge in $ G $ belongs to one of $ N+1 $ types, ranging from type $ 0 $ to type $ N $ . For type $ i $ $ (0 \le i \le N) $ , there are exactly $ 2^i $ edges, which are numbered $ 2^i+0, 2^i+1, \dots, 2^i+(2^i-1) $ . The edge numbered $ 2^i + j $ $ (0 \leq j \leq 2^i - 1) $ is an undirected edge of length $ C_{2^i + j} $ that connects vertex $ j \times 2^{N-i} $ and vertex $ (j+1) \times 2^{N-i} $ . 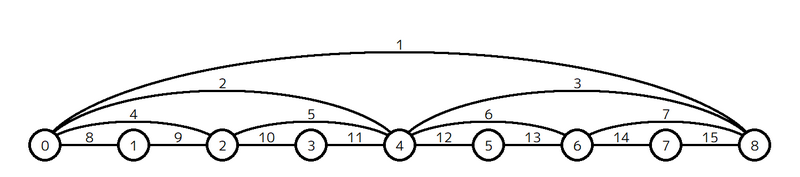For example, when $ N = 3 $ , $ G $ looks like the following graph:  You are given $ Q $ queries to process. There are two types of queries: - `1 j x`: Change the length of edge $ j $ to $ x $ . - `2 s t`: Find the shortest path length from vertex $ s $ to vertex $ t $ .

The input is given in the following format. Note that vertex numbering starts from $ 0 $ , while edge numbering starts from $ 1 $ . > $ N $ $ C_1 $ $ C_2 $ $ \cdots $ $ C_{2^{N+1}-1} $ $ Q $ $ \text{query}_1 $ $ \text{query}_2 $ $ \vdots $ $ \text{query}_Q $ Here, $ \text{query}_i $ represents the $ i $ -th query. Each query is given in one of the following formats: > 1 $ j $ $ x $ > 2 $ s $ $ t $

Let $ m $ be the number of queries of type `2 s t`. Output $ m $ lines, where the $ i $ -th line contains the answer to the $ i $ -th `2 s t` query.

### Partial Score $ 30 $ points will be awarded for passing the testset satisfying the additional constraint: There is no `1 j x` query. ### Sample Explanation 1 - In the 1st query, using edge $ 8 $ , the path $ 0 \to 1 $ results in a total distance of $ 2 $ . - In the 2nd query, using edge $ 2 $ , the path $ 0 \to 4 $ results in a total distance of $ 1 $ . - In the 3rd query, using edge $ 6 $ , the path $ 4 \to 6 $ results in a total distance of $ 4 $ . - In the 4th query, using edges $ 2, 1 $ , the path $ 4 \to 0 \to 8 $ results in a total distance of $ 8 $ . - In the 5th query, using edges $ 11, 6, 13 $ , the path $ 3 \to 4 \to 6 \to 5 $ results in a total distance of $ 17 $ . - In the 6th query, the length of edge $ 6 $ is updated from $ 4 $ to $ 30 $ . - In the 7th query, using edges $ 11, 12 $ , the path $ 3 \to 4 \to 5 $ results in a total distance of $ 18 $ . - In the 8th query, using edges $ 2, 1, 15, 14 $ , the path $ 4 \to 0 \to 8 \to 7 \to 6 $ results in a total distance of $ 13 $ . - In the 9th query, the length of edge $ 1 $ is updated from $ 7 $ to $ 10000000 $ . - In the 10th query, using edges $ 2, 3 $ , the path $ 0 \to 4 \to 8 $ results in a total distance of $ 15 $ . ### Constraints - All input values are integers. - $ 1 \le N \le 18 $ - $ 1 \le C_j \le 10^7 $ $ (1 \le j \le 2^{N+1}-1) $ - $ 1 \le Q \le 2 \times 10^5 $ - In the query `1 j x`, $ 1 \le j \le 2^{N+1}-1 $ and $ 1 \le x \le 10^7 $ . - In the query `2 s t`, $ 0 \le s < t \le 2^N $ . - There is at least one `2 s t` query.