AT_tupc2022_f Block Rotation

有一个 $N \times N$ 的格子。对于 $i = 1,2,\dots,N$，从左起第 $i$ 列的最底部有 $M_i$ 个 $1 \times 1$ 的正方形小方块，每个方块都被涂上了颜色。这里 $M_1,M_2,\dots,M_N$ 是单调不增的。对于从左起第 $i$ 列，从下往上第 $j$ 个方块被涂上了颜色 $C_{i,j}$。 对于格子，考虑如下操作： - 将整个格子顺时针瞬间旋转 $90^\circ$，然后所有有颜色的方块会根据重力“同时下落”。更为形式化地说，对于从左起第 $i$ 列从下往上第 $j$ 个方块，若与其同高、且在其右侧的方块有 $c_{i,j}$ 个（包括颜色为 $0$ 的空格子），则该方块会被移动到从左起第 $j$ 列，从下往上第 $c_{i,j}+1$ 个格子。此移动会对所有方块同时进行。 请问最少需要多少次操作，格子才能回到刚开始的状态？请输出对 $998244353$ 取模后的结果。 格子配置的相同的定义如下： 将格子的配置对应为一个 $N \times N$ 的矩阵 $A$。$A_{i,j} \ (i,j=1,2,\dots,N)$ 的定义如下： - 若从左起第 $i$ 列从下往上第 $j$ 个格子中有方块，则其值为方块的颜色，否则为 $0$。 两次格子的配置相同，当且仅当它们对应的矩阵 $A$ 完全相同。

输入以如下格式从标准输入读入。 > $N$ $M_1$ $C_{1,1}$ $C_{1,2}$ $\dots$ $C_{1,M_1}$ $M_2$ $C_{2,1}$ $C_{2,2}$ $\dots$ $C_{2,M_2}$ > $\vdots$ > $M_N$ $C_{N,1}$ $C_{N,2}$ $\dots$ $C_{N,M_N}$

输出操作次数的最小值，对 $998244353$ 取模后的结果。

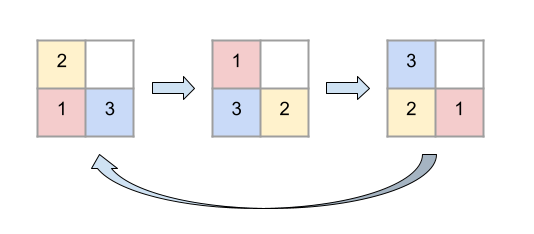
### 样例解释 1 通过操作，颜色的分布将如下变化。本例中，经过 $3$ 次操作后，状态会回到最初的状态。  ### 数据范围 - $2 \leq N \leq 10^5$ - $1 \leq \displaystyle \sum_{i=1}^N M_i \leq 10^5$ - $N \geq M_1 \geq M_2 \geq \dots \geq M_N \geq 0$ - $1 \leq C_{i,j} \leq 10^5$ - 所有输入均为整数。 由 ChatGPT 5 翻译