AT_tupc2022_f Block Rotation

$ N \times N $ のマス目があります。 $ i = 1,2,\dots,N $ について、左から $ i $ 列目には下から $ M_i $ 個の $ 1 \times 1 $ の正方形のブロックがあり、それぞれのブロックには色が塗られています。ここで、 $ M_1,M_2,\dots,M_N $ は単調非増加です。左から $ i $ 列目の下から $ j $ 個目のブロックには色 $ C_{i,j} $ が塗られています。 マス目に対して、以下のような操作を考えます。 - マス目を時計回りに瞬間的に $ 90^\circ $ 回転させた後、色のついたブロックを重力に従って同時に落下させる。より形式的には、左から $ i $ 列目の下から $ j $ 個目のブロックについて、そのブロックと同じ高さでそのブロックよりも右にあるブロックが $ c_{i,j} $ 個あるとすると、このブロックを左から $ j $ 列目の下から $ c_{i,j}+1 $ 番目のマスに移動させる。この移動は全てのブロックに対して同時に行う。 マス目が最初の配置に戻ってくるまでに、最小で何回の操作が必要でしょうか？ $ 998244353 $ で割った余りを求めてください。 マス目の配置の一致性の定義 マス目の配置に対して、 $ N \times N $ 行列 $ A $ を対応させる。 $ A_{i,j} \, (i,j=1,2,\dots,N) $ は次のようにして定める。 - マス目の左から $ i $ 列目の下から $ j $ 番目のマスにブロックが存在すればその色、存在しなければ $ 0 $ $ 2 $ つのマス目の配置が一致するとは、それぞれの配置に対応する行列 $ A $ が一致することである。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M_1 $ $ C_{1,1} $ $ C_{1,2} $ $ \dots $ $ C_{1,M_1} $ $ M_2 $ $ C_{2,1} $ $ C_{2,2} $ $ \dots $ $ C_{2,M_2} $ $ \vdots $ $ M_N $ $ C_{N,1} $ $ C_{N,2} $ $ \dots $ $ C_{N,M_N} $

答えを $ 998244353 $ で割った余りを出力せよ。

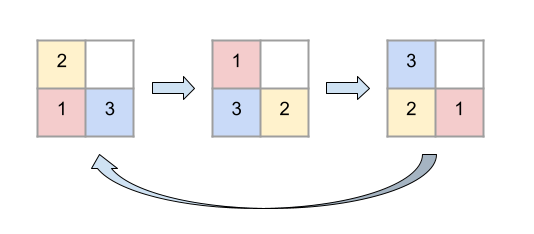
### Sample Explanation 1 操作によって色の配置は以下のように変化します。この例では、 $ 3 $ 回の操作で元の状態に戻ります。  ### Constraints - $ 2 \leq N \leq 10^5 $ - $ 1 \leq \displaystyle \sum_{i=1}^N M_i \leq 10^5 $ - $ N \geq M_1 \geq M_2 \geq \dots \geq M_N \geq 0 $ - $ 1 \leq C_{i,j} \leq 10^5 $ - 入力はすべて整数