AT_tupc2022_j AMidA

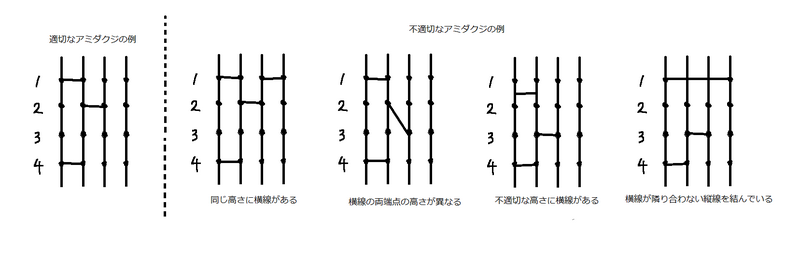
$ N $ 本の縦線からなるアミダクジがあります。 それぞれの縦線の長さは $ 2M+1 $ $ [\mathrm{cm}] $ であり、横線は以下の条件を満たす必要があります。 - 横線の端点となれるのは上から $ 1,2,\dots,2M $ $ [\mathrm{cm}] $ の高さのみであり、横線の両端点の高さは等しい - 全ての横線は、隣り合う $ 2 $ つの縦線のみを繋ぐ - 同じ高さにある横線は高々 $ 1 $ 本  初め、このアミダクジに $ M $ 本の横線がひかれています。 $ j\ (j=1,2,\dots,M) $ 本目の横線は、上から $ 2j $ $ [\mathrm{cm}] $ の位置にひかれており、左から $ a_j $ 本目の縦線と $ a_j+1 $ 本目の縦線を結んでいます。 このアミダクジに以下の操作を任意の回数 ( $ 0 $ 回も可) 行う事が出来ます。 - まだ横線のひかれていない高さ $ h $ 及び、 $ 1 $ 以上 $ N-1 $ 以下の整数 $ b $ を選ぶ。 上から $ h $ $ [\mathrm{cm}] $ の位置に左から $ b $ 本目の縦線と $ b+1 $ 本目の縦線を結ぶ横線を追加する。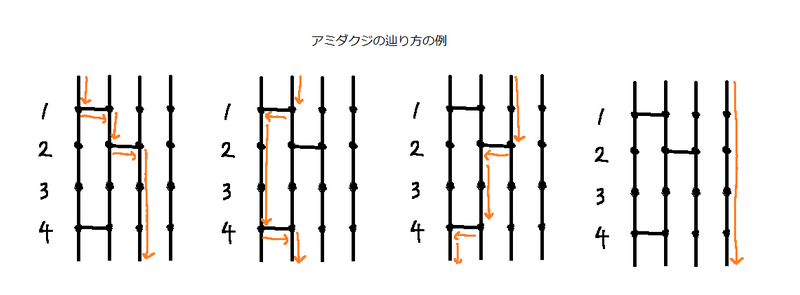 すべての $ i=1,2,\dots,N $ に対して左から $ i $ 本目の縦線からクジを辿り始めると結果が左から $ i $ 本目となるアミダクジを 「**恒等的なアミダクジ**」 と呼ぶとき、与えられたアミダクジを恒等的なアミダクジにするために必要な最小の操作回数を求めてください。 また、最小の操作回数を達成する操作の方法を $ 1 $ つ示してください。 この制約の元、恒等的なアミダクジにする操作方法が常に存在することが示せます。 

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ a_1 $ $ a_2 $ $ \dots $ $ a_M $

必要な操作回数の最小値を $ ans $ として、 $ 1+ans $ 行で出力せよ。 $ 1 $ 行目には $ ans $ を出力せよ。 続く $ j+1\ (j=1,2,\dots,ans) $ 行目には $ j $ 回目の操作で上から $ h_j $ $ [\mathrm{cm}] $ の位置に左から $ b_j $ 本目の縦線と $ b_j+1 $ 本目の縦線を結ぶ横線を追加するとして、 $ h_j,b_j $ をこの順に空白区切りで出力せよ。

### Sample Explanation 1 他にも、 ``` 2 1 2 3 1 ``` を出力しても正解となります。 ### Sample Explanation 3 操作をしなくても恒等的なアミダクジになっている場合もあります。 ### Constraints - $ 2 \leq N \leq 2\times10^5 $ - $ 1\leq M\leq 2\times10^5 $ - $ 1 \leq a_j < N\ (j=1,2,\dots,M) $ - 入力はすべて整数