AT_tupc2022_j AMidA

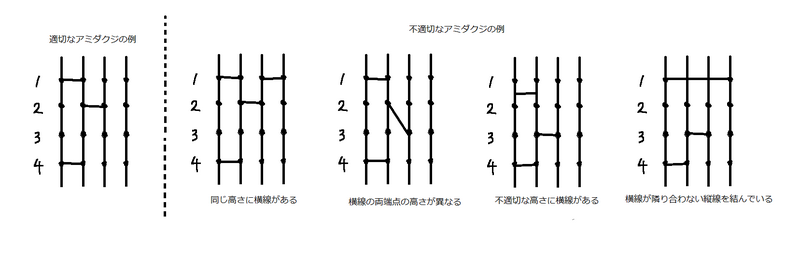
有一个由 $N$ 条竖线组成的阿弥陀签。每条竖线的长度为 $2M+1\ [\mathrm{cm}]$，横线需要满足下列条件： - 横线的端点只能出现在从上往下数的 $1,2,\dots,2M\ [\mathrm{cm}]$ 高度上，并且横线两端的高度需相等。 - 所有横线仅连接相邻的 $2$ 条竖线。 - 在同一高度上至多只能有 $1$ 条横线。  初始情况下，该阿弥陀签有 $M$ 条横线。第 $j$ $(j=1,2,\dots,M)$ 条横线画在从上往下数第 $2j\ [\mathrm{cm}]$ 的位置，连接从左往右数第 $a_j$ 条竖线和第 $a_j+1$ 条竖线。 对于这个阿弥陀签，可以进行任意次（$0$ 次也可以）如下操作： - 选择尚未被画横线的高度 $h$，以及 $1\leq b\leq N-1$ 的整数 $b$。在从上往下数第 $h\ [\mathrm{cm}]$ 的位置，添加连接从左往右数第 $b$ 条和第 $b+1$ 条竖线的横线。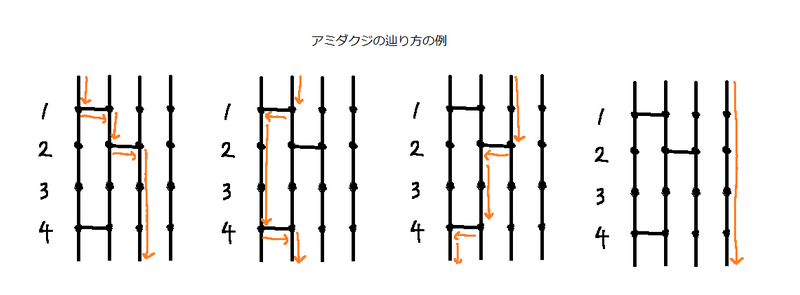 若对于所有 $i=1,2,\dots,N$，从左往右数第 $i$ 条竖线出发，结果都在左边第 $i$ 条竖线结束，则称该阿弥陀签为“恒等的阿弥陀签”。请你求出，为了把给定的阿弥陀签变成恒等的阿弥陀签，最少需要进行多少次操作，并给出一种达到最小操作次数的方案。 在本题约束条件下，始终存在能将其变为恒等的阿弥陀签的操作方案。 

输入格式如下所示，通过标准输入给出。 > $N$ $M$ $a_1$ $a_2$ $\dots$ $a_M$

请输出最小操作次数 $ans$，共 $1+ans$ 行。 第 $1$ 行输出 $ans$。接下来的 $j+1$ 行（$j=1,2,\dots,ans$），每行输出 $h_j\ b_j$，表示第 $j$ 次操作在从上往下数第 $h_j\ [\mathrm{cm}]$ 处添加一条连接左起第 $b_j$ 条与第 $b_j+1$ 条竖线的横线。各元素之间用空格隔开。

### 样例解释 1 此外，输出 ``` 2 1 2 3 1 ``` 也是可以的。 ### 样例解释 3 在有些情况下，不进行操作也已经是恒等的阿弥陀签了。 ### 数据范围 - $2 \leq N \leq 2\times 10^5$ - $1\leq M\leq 2\times 10^5$ - $1 \leq a_j < N\ (j=1,2,\dots,M)$ - 所有输入均为整数。 由 ChatGPT 5 翻译