AT_tupc2022_m Fractal Tree Isomorphism
题目描述
对于一棵有根树 $S$,定义 $f(S)$ 为如下操作后的有根树:
- 用树 $S$ 自身替换 $S$ 的所有叶子节点。
对于有根树 $S$,定义一组无穷序列的树 $(S_1, S_2, \dots)$,具体为:
- $S_1 := S$
- $S_i := f(S_{i-1}) \quad (i > 1)$
定义无穷树 $S_{\infty}:= \displaystyle\lim_{n\to\infty} S_n$,称其为由 $S$ 导出的**分形树**(fractal tree)。
---
给定 $K$ 棵有根树 $T_1, T_2, \dots, T_K$。每棵树 $T_i\,(i=1,2,\dots,K)$ 满足以下条件:
- 顶点数为 $N_i \geq 2$
- 顶点依次编号为 $1,2,\dots,N_i$
- 根为编号 $1$ 的顶点
- 对于 $j=2,3,\dots,N_i$,顶点 $j$ 的父节点为 $p_{i,j}$
请对于每一对 $(i,j) \, (i,j=1,2,\dots,K)$,判断由 $T_i,T_j$ 各自导出的分形树 $(T_i)_\infty$ 和 $(T_j)_\infty$ 是否同构。
分形树的同构定义如下:
记分形树 $T$ 的顶点集合为 $V(T)$,边集合为 $E(T)$。若存在一个双射 $\varphi:V(S)\to V(T)$,使得以下两个条件成立,则称两棵分形树 $S,T$ 同构:
- $\{u,v\}\in E(S) \iff \{\varphi(u),\varphi(v)\}\in E(T)$
- $S,T$ 的根节点分别为 $r_S, r_T$ 时,$\varphi(r_S)=r_T$
输入格式
输入格式如下,经标准输入给出:
> $K \ N_1 \ p_{1,2} \ p_{1,3} \ \dots \ p_{1,N_1} \ N_2 \ p_{2,2} \ p_{2,3} \ \dots \ p_{2,N_2} \ \vdots\ N_K \ p_{K,2} \ p_{K,3} \ \dots \ p_{K,N_K}$
输出格式
输出 $K$ 行。第 $i$ 行输出长度为 $K$ 的仅由 `0` 或 `1` 组成的字符串。
第 $i$ 行的第 $j$ 个字符,如果 $(T_i)_\infty$ 和 $(T_j)_\infty$ 同构则为 `1`,否则为 `0`。
说明/提示
### 样例解释 1
给定的树如下所示。
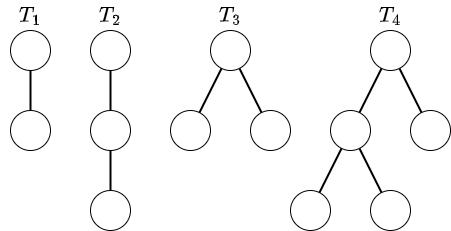
对这些树进行一次操作后的结果如下所示。
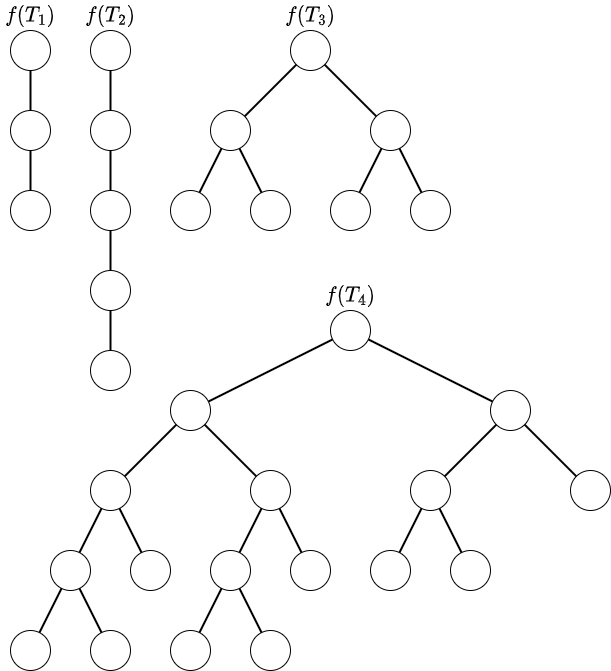
### 数据范围
- $2 \leq K \leq 1000$
- $2 \leq N_i \leq 5\times 10^4 \quad (1\leq i\leq K)$
- $\displaystyle\sum_{i=1}^K N_i \leq 10^5$
- $1 \leq p_{i,j} < j \quad (1 \leq i \leq K,\,2\leq j \leq N_i)$
- 所有输入均为整数。
由 ChatGPT 5 翻译