AT_tupc2022_m Fractal Tree Isomorphism

根付き木 $ S $ に対して、根付き木 $ f(S) $ を、 $ S $ に対して次の操作を行ったものとします。 - 木 $ S $ の葉をすべて $ S $ 自身で置き換える 根付き木 $ S $ に対して、木の無限列 $ (S_1, S_2, \dots) $ を次のようにして定義します。 - $ S_1 := S $ - $ S_i := f(S_{i-1}) \quad (i > 1) $ 無限木 $ S_{\infty}:= \displaystyle\lim_{n\to\infty} S_n $ を $ S $ から誘導される **fractal tree** と呼びます。 --- $ K $ 個の根付き木 $ T_1, T_2, \dots, T_K $ が与えられます。 $ T_i\,(i=1,2,\dots,K) $ は、以下の条件をみたす根付き木です。 - 頂点数は $ N_i \geq 2 $ - 頂点には $ 1,2,\dots,N_i $ の番号が付けられている - 根は頂点 $ 1 $ である - $ j=2,3,\dots,N_i $ について、頂点 $ j $ の親は頂点 $ p_{i,j} $ である 各 $ (i,j) \, (i,j=1,2,\dots,K) $ について、 $ T_i,\,T_j $ からそれぞれ誘導される fractal tree $ (T_i)_\infty $ と $ (T_j)_\infty $ が同型か判定してください。 Fractal tree の同型性の定義 Fractal tree $ T $ の頂点集合を $ V(T) $ 、辺集合を $ E(T) $ とする。2 つの fractal tree $ S,T $ が同型であるとは、以下の 2 つの条件を満たす全単射 $ \varphi:V(S)\to V(T) $ が存在することである。 - $ \{u,v\}\in E(S) \iff \{\varphi(u),\varphi(v)\}\in E(T) $ - $ S,T $ の根をそれぞれ $ r_S, r_T $ としたとき、 $ \varphi(r_S)=r_T $

入力は以下の形式で標準入力から与えられる。 > $ K $ $ N_1 $ $ p_{1,2} $ $ p_{1,3} $ $ \dots $ $ p_{1,N_1} $ $ N_2 $ $ p_{2,2} $ $ p_{2,3} $ $ \dots $ $ p_{2,N_2} $ $ \vdots $ $ N_K $ $ p_{K,2} $ $ p_{K,3} $ $ \dots $ $ p_{K,N_K} $

$ K $ 行出力せよ。 $ i $ 行目には、長さ $ K $ の `0` または `1` からなる文字列を出力せよ。 $ i $ 行目の $ j $ 文字目は、 $ (T_i)_\infty $ と $ (T_j)_\infty $ が同型なら `1`、同型でないなら `0` とせよ。

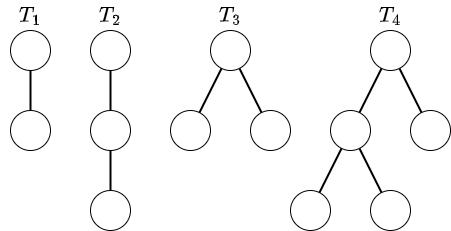
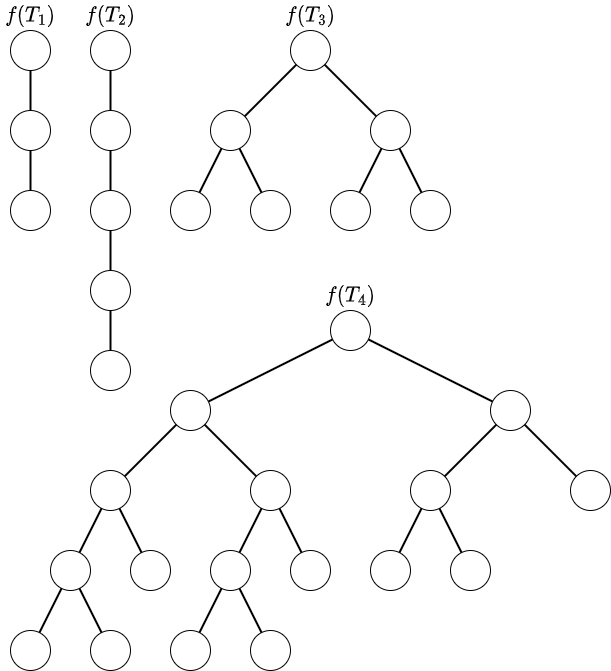
### Sample Explanation 1 与えられる木は以下の通りです。  これらの木に $ 1 $ 回操作を施した木は以下の通りです。  ### Constraints - $ 2 \leq K \leq 1000 $ - $ 2 \leq N_i \leq 5 \times 10^4 \quad (1 \leq i \leq K) $ - $ \displaystyle\sum_{i=1}^K N_i \leq 10^5 $ - $ 1 \leq p_{i,j} < j \quad (1 \leq i \leq K,\,2\leq j \leq N_i) $ - 入力はすべて整数