AT_tupc2023_a Namboku / Tozai Line

在二维平面上有 $N$ 个城市。第 $i$ 个城市位于坐标 $(x_i, y_i)$，人口为 $p_i$。 你需要从中选择一个城市，将该城市作为基点，沿着与 $x$ 轴平行（东西方向）和 $y$ 轴平行（南北方向）各修建一条无限延伸的地铁线。 请通过适当选择基点城市，求能乘坐地铁的最大人数。这里，能乘坐地铁的人是指所有在地铁经过的城市中的人口总数（即所有在地铁经过的城市中居住的人）。

输入以如下格式从标准输入读入。 >$N$ >$x_1$ $y_1$ $p_1$ >$x_2$ $y_2$ $p_2$ >$\vdots$ >$x_N$ $y_N$ $p_N$

输出能乘坐地铁的最大人数。

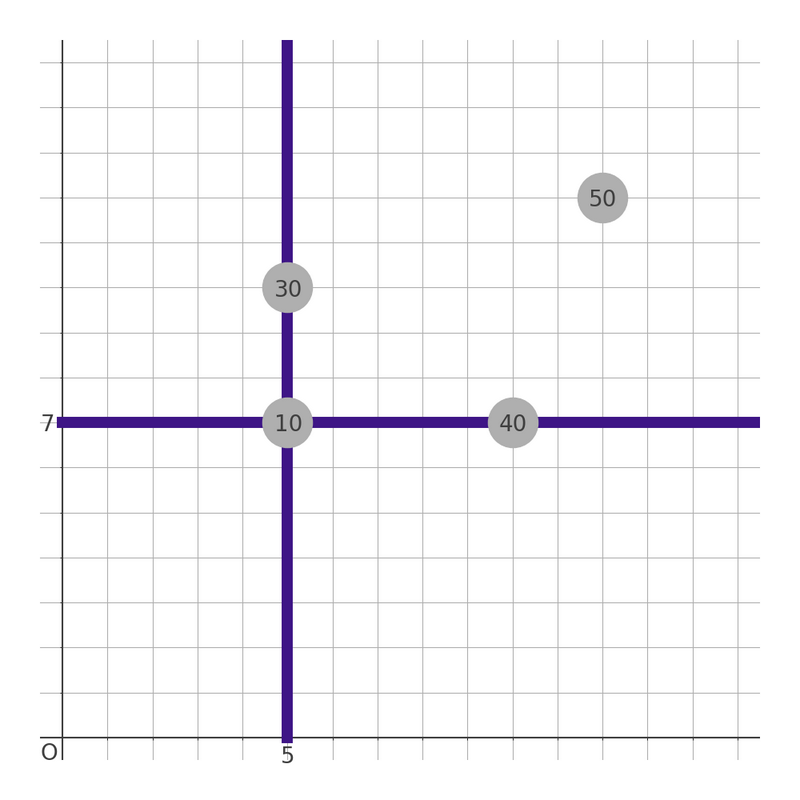
## 背景 在仙台，以仙台站为中心有两条地铁线路，分别是南北线和东西线。（[wikipedia / 仙台市地下铁](https://ja.wikipedia.org/wiki/%E4%BB%99%E5%8F%B0%E5%B8%82%E5%9C%B0%E4%B8%8B%E9%89%84)） ## 样例解释 1 如果选择第 $3$ 个城市作为基点，则会沿直线 $x = 5, y = 7$ 建设地铁。此时，城市 $1$、城市 $3$、城市 $4$ 上居住的人口 $40 + 10 + 30 = 80$ 人都可以使用地铁，这就是最大值。  ## 样例解释 2 请注意，无法以坐标 $(1, 3)$ 作为基点建设地铁。 ## 样例解释 3 注意，答案可能超过 $32$ 位整数的范围。 ## 数据范围 - $1 \leq N \leq 2 \times 10^5$ - $1 \leq x_i, y_i \leq 2 \times 10^5$ - $1 \leq p_i \leq 10^9$ - $(x_i, y_i) \neq (x_j, y_j)\ (i \neq j)$ - 所有输入均为整数。 由 ChatGPT 5 翻译