AT_tupc2023_a Namboku / Tozai Line

$ 2 $ 次元平面上に $ N $ 個の都市があります。 $ i $ 番目の都市は座標 $ (x_i, y_i) $ に位置し、人口が $ p_i $ 人です。 あなたは都市を一つ選び、選んだ都市を基点として（ $ x $ 軸に平行な）東西方向・（ $ y $ 軸に平行な）南北方向に無限に伸びる地下鉄を敷設しようと考えています。 都市を適切に選ぶことで、地下鉄を利用できる人数の最大値を求めてください。 ただし、地下鉄を利用できる人とは、地下鉄が通る都市に住むすべての人を指します。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ x_1 $ $ y_1 $ $ p_1 $ $ x_2 $ $ y_2 $ $ p_2 $ $ \vdots $ $ x_N $ $ y_N $ $ p_N $

地下鉄を利用できる人数の最大値を出力してください。

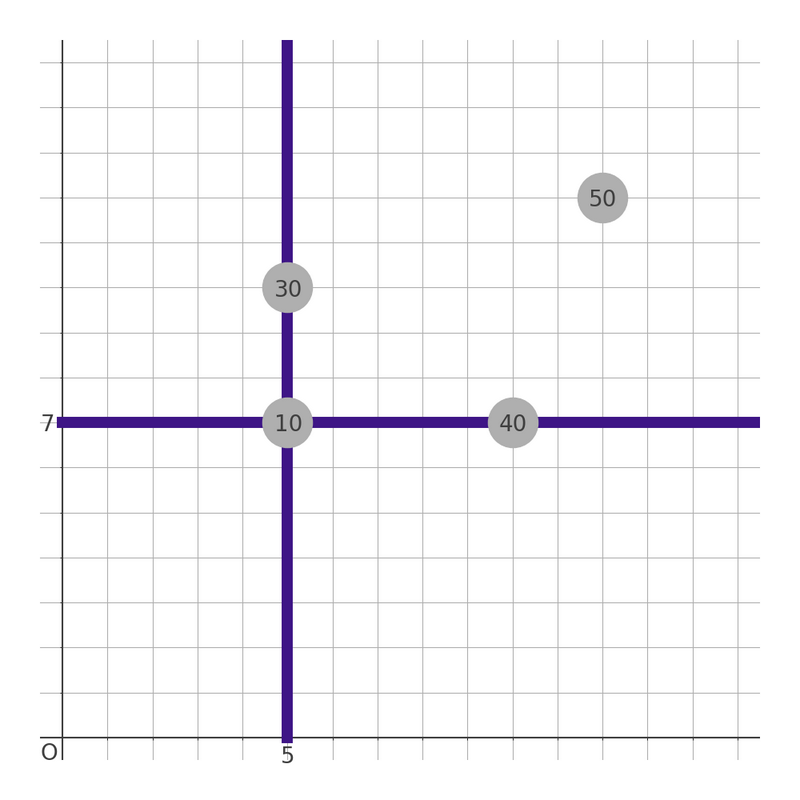
### 背景 仙台には仙台駅を中心に南北線・東西線という $ 2 $ 本の地下鉄が通っています。 ( [wikipedia / 仙台市地下鉄](https://ja.wikipedia.org/wiki/%E4%BB%99%E5%8F%B0%E5%B8%82%E5%9C%B0%E4%B8%8B%E9%89%84) ) ### Sample Explanation 1 $ 3 $ 番目の都市を選ぶと、直線 $ x = 5, y = 7 $ 上に地下鉄が敷設されます。 このとき、都市 $ 1 $ 、都市 $ 3 $ 、都市 $ 4 $ に住む $ 40 + 10 + 30 = 80 $ 人が地下鉄を利用でき、これが最大値となります。  ### Sample Explanation 2 座標 $ (1, 3) $ を基点とする地下鉄は敷設できないことに注意してください。 ### Sample Explanation 3 答えは $ 32 $ bit 整数型に収まらない場合があります。 ### Constraints - $ 1 \leq N \leq 2 \times 10^5 $ - $ 1 \leq x_i, y_i \leq 2 \times 10^5 $ - $ 1 \leq p_i \leq 10^9 $ - $ (x_i, y_i) \neq (x_j, y_j) \, (i \neq j) $ - 入力はすべて整数