AT_tupc2023_c Topological Sort

$ (1,2,\ldots,N) $ の順列を以下では単に順列と呼びます。 正整数 $ N $ と順列 $ P $ が与えられます。 有向閉路と多重辺を持たない、頂点に $ 1 $ から $ N $ までの番号が付けられ、辺に番号が付けられていない $ N $ 頂点の有向グラフであって、辞書順最小トポロジカル順序が $ P $ と一致するようなものの個数を $ 998244353 $ で割った余りを求めてください。 辞書順最小トポロジカル順序の定義 順列 $ Q $ と（頂点に $ 1 $ から $ N $ までの番号が付けられている） $ N $ 頂点の有向グラフ $ G $ が以下の条件を満たすとき、 $ Q $ は $ G $ のトポロジカル順序であると言います。 - $ G $ の各有向辺 $ e=(u,v) $ （ $ u $ が始点、 $ v $ が終点）に対して、 $ u $ は $ Q $ において $ v $ よりも先に現れる $ G $ が有向閉路を持たないとき、 $ G $ のトポロジカル順序であるような順列が必ず存在することが証明でき、それらのうち辞書順最小のものを辞書順最小トポロジカル順序と言います。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ P_1 $ $ P_2 $ $ \ldots $ $ P_N $

答えを出力せよ。

### Sample Explanation 1 以下の $ 4 $ つの有向グラフが条件を満たします。 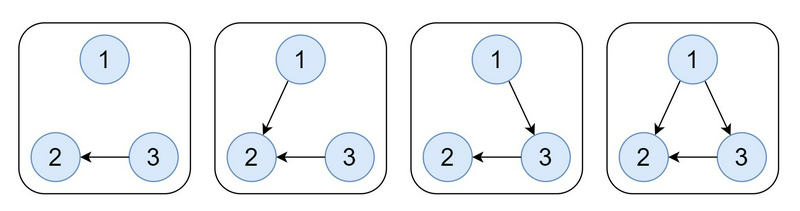 ### Constraints - $ 2\leq N\leq 2\times 10^5 $ - $ (P_1, P_2, \ldots,P_N) $ は $ (1,2, \ldots,N) $ の順列 - 入力はすべて整数