AT_tupc2023_c Topological Sort

我们将 $ (1,2,\ldots,N) $ 的排列简称为“顺序排列”。 给定正整数 $ N $ 和一个顺序排列 $ P $。 请你求出有多少个 $ N $ 个顶点的有向图（顶点编号为 $ 1 $ 到 $ N $，图中没有有向环和重边，边没有编号），其字典序最小的拓扑序等于 $ P $。将答案对 $ 998244353 $ 取余后输出。 **字典序最小拓扑序的定义：** 对于顺序排列 $ Q $ 和一个 $ N $ 个顶点的有向图 $ G $（顶点编号为 $ 1 $ 到 $ N $），如果满足以下条件，则称 $ Q $ 是 $ G $ 的一个拓扑序： - 对于 $ G $ 的每一条有向边 $ e=(u,v) $（$ u $ 为起点，$ v $ 为终点），在 $ Q $ 中 $ u $ 必须出现在 $ v $ 之前。 可以证明，如果 $ G $ 没有有向环，则必定存在至少一个拓扑序。从所有拓扑序中字典序最小的那个称为 $ G $ 的字典序最小拓扑序。

输入由一行给出，格式如下： > $ N\ P_1\ P_2\ \ldots\ P_N $

请输出答案。

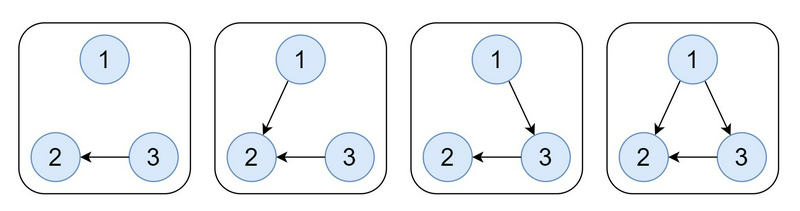
### 样例解释 1 如下的 $ 4 $ 个有向图均满足题意。  ### 数据范围 - $ 2\leq N\leq 2\times 10^5 $ - $ (P_1, P_2, \ldots,P_N) $ 是 $ (1,2,\ldots,N) $ 的一个排列 - 输入均为整数 由 ChatGPT 5 翻译