AT_tupc2024_g Convex Hull of Intersections

$ xy $ 平面上に相異なる $ N $ 本の直線があり、 $ i $ 番目の直線 $ \ell_i $ は $ a_i x + b_i y + c_i = 0 $ の形で表されます。 これらの直線群の交点全体の集合を $ P $ とします。より厳密には次の通りです。 $ P = \{ p \in \mathbb{R}^2 \mid \exists i, j \in \{1, 2, \ldots, N\} \, \text{ s.t. } \, p \in \ell_i, \, p \in \ell_j, \, i \neq j \} $ このとき、 $ P $ の凸包の面積を求めてください。ただし、凸包が空集合、1 点集合または線分である場合、その面積は $ 0 $ とします。 凸包の定義 有限集合 $ S = \{ x_1, \ldots, x_{|S|} \} $ の凸包 $ \text{conv}(S) $ を次で定めます。 $ \displaystyle \text{conv}(S) = \left\{ \sum_{i=1}^{|S|} \alpha_i x_i \, \middle\vert \, \sum_{i=1}^{|S|} \alpha_i = 1, \, 0 \leq \alpha_i \leq 1 \right\} $ $ T $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。

入力は以下の形式で標準入力から与えられる。 > $ T $ $ \text{case}_1 $ $ \text{case}_2 $ $ \vdots $ $ \text{case}_T $ ここで $ \text{case}_i $ は $ i $ 番目のテストケースを表し、各テストケースは以下の形式で与えられる。 > $ N $ $ a_1 $ $ b_1 $ $ c_1 $ $ a_2 $ $ b_2 $ $ c_2 $ $ \vdots $ $ a_N $ $ b_N $ $ c_N $

$ T $ 行出力せよ。 $ i $ 行目には $ i $ 番目のテストケースの答えを出力せよ。 真の解との絶対誤差または相対誤差が $ {10}^{-5} $ 以下のとき正解と判定される。

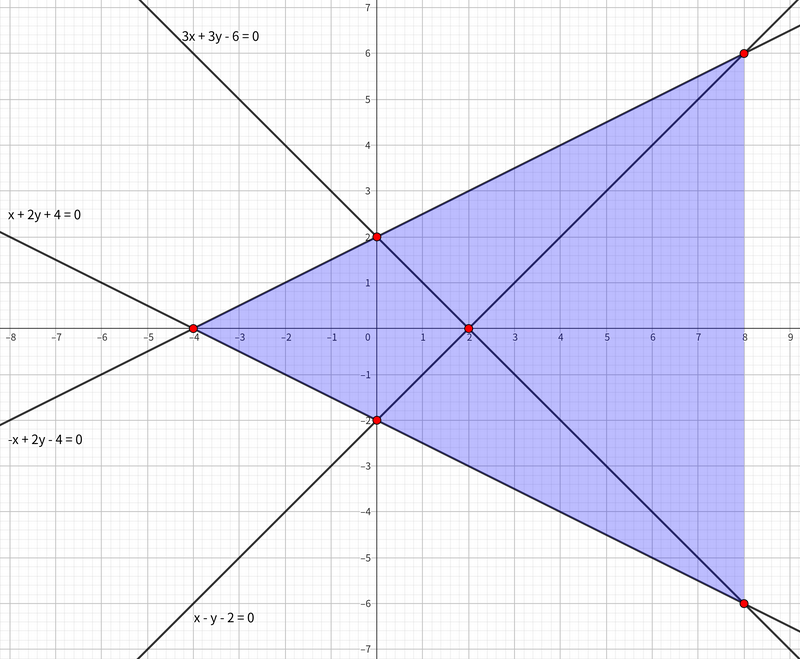
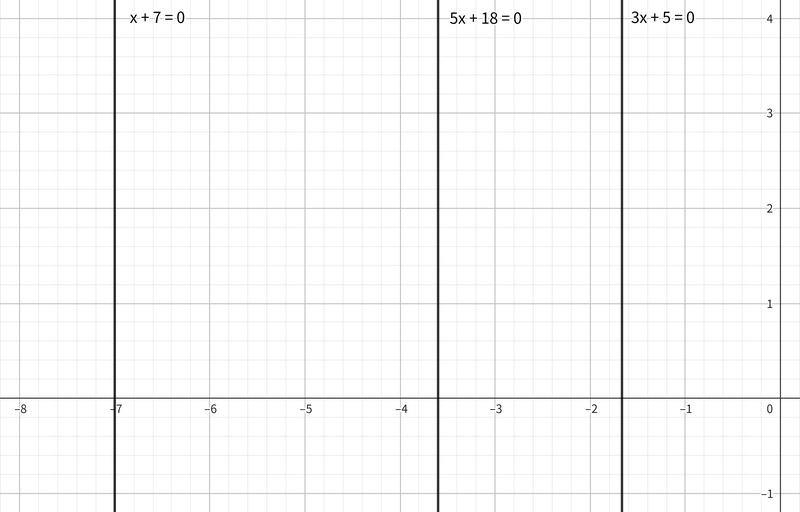
### Sample Explanation 1 $ 1 $ つ目のテストケースでは、 $ P $ の凸包は $ (8, 6), (-4, 0), (8, -6) $ をこの順に結ぶ三角形であり、その面積は $ 72 $ です。 $ 2 $ つ目のテストケースでは、 $ 3 $ つの直線は全て平行なため $ P = \emptyset $ です。 したがって、 $ P $ の凸包の面積は $ 0 $ です。   ### Constraints - $ 1 \leq T $ - $ 2 \leq N \leq {10}^4 $ - $ |a_i|, |b_i|, |c_i| \leq {10}^3 $ - $ a_i \neq 0 $ または $ b_i \neq 0 $ - 直線 $ \ell_i $ と $ \ell_j $ は異なる ( $ i \neq j $ ) - $ 1 $ つの入力ファイルに含まれる $ N $ の総和は $ 2 \times {10}^5 $ 以下 - 入力はすべて整数