AT_tupc2024_g Convex Hull of Intersections

在 $xy$ 平面上有 $N$ 条互不相同的直线，第 $i$ 条直线 $\ell_i$ 可以表示为 $a_i x + b_i y + c_i = 0$ 的形式。所有这些直线的交点的集合记为 $P$。更严格地说，定义如下： $$ P = \left\{ p \in \mathbb{R}^2 \mid \exists \, i, j \in \{1, 2, \ldots, N\} \text{ 且 } i \neq j, \, p \in \ell_i, \, p \in \ell_j \right\} $$ 请计算 $P$ 的凸包的面积。如果凸包为空集、只有一个点或是一条线段，则认为面积为 $0$。 凸包的定义 有限集合 $S = \{ x_1, \ldots, x_{|S|} \}$ 的凸包 $\text{conv}(S)$ 定义如下： $$ \text{conv}(S) = \left\{ \sum_{i=1}^{|S|} \alpha_i x_i \,\middle|\, \sum_{i=1}^{|S|} \alpha_i = 1, \; 0 \leq \alpha_i \leq 1 \right\} $$ 给定 $T$ 组测试数据，请分别给出每组的答案。

输入按以下格式从标准输入读入。 > $T$ > $\text{case}_1$ > $\text{case}_2$ > $\vdots$ > $\text{case}_T$ 其中，$\text{case}_i$ 表示第 $i$ 个测试用例，每个测试用例的格式如下： > $N$ > $a_1$ $b_1$ $c_1$ > $a_2$ $b_2$ $c_2$ > $\vdots$ > $a_N$ $b_N$ $c_N$

输出 $T$ 行，第 $i$ 行输出第 $i$ 个测试用例的答案。 当且仅当你的答案与标准答案在绝对误差或相对误差不超过 $10^{-5}$ 时，会被判定为正确。

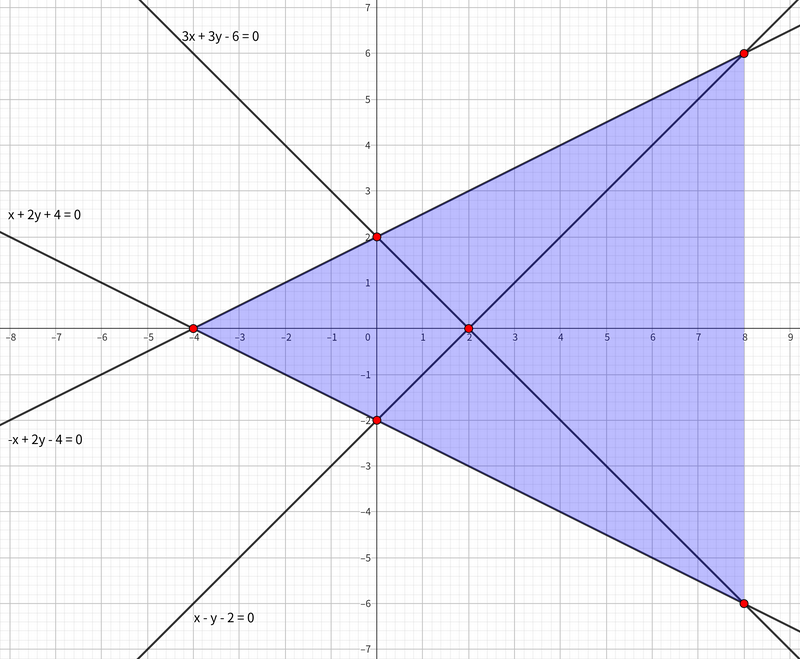
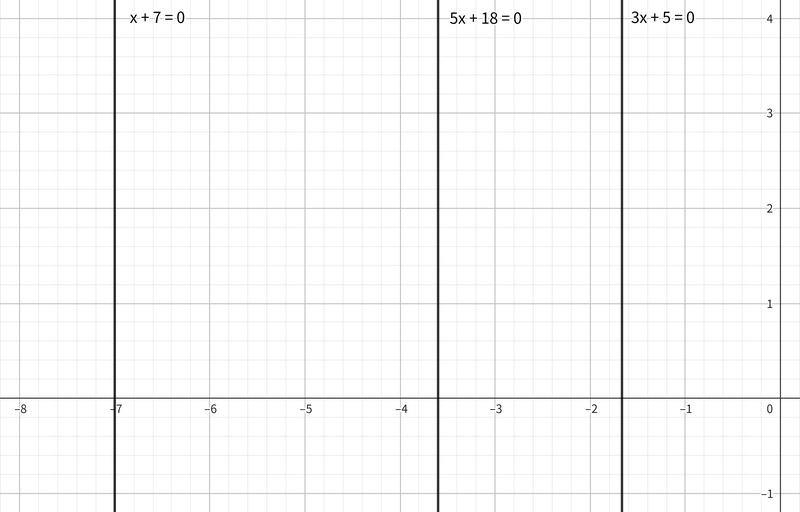
### 样例解释 1 第 $1$ 个测试用例中，$P$ 的凸包是依次连接 $(8, 6), (-4, 0), (8, -6)$ 形成的三角形，其面积为 $72$。 第 $2$ 个测试用例，三条直线均互相平行，因此 $P = \emptyset$。所以 $P$ 的凸包面积为 $0$。   ### 数据范围 - $1 \leq T$ - $2 \leq N \leq 10^4$ - $|a_i|, |b_i|, |c_i| \leq 10^3$ - 至少有一个 $a_i \neq 0$ 或 $b_i \neq 0$ - 任意 $i \neq j$，直线 $\ell_i$ 与 $\ell_j$ 不相同 - 同一份输入文件中所有 $N$ 的总和不超过 $2 \times 10^5$ - 输入均为整数 由 ChatGPT 5 翻译