AT_tupc2024_i Small Steps

頂点に $ 1 $ から $ n $ までの番号がついた $ n $ 頂点の木 $ t $ に対し、以下の条件を満たす $ (1, \dots, n) $ の順列 $ p = (p_1, \dots, p_n) $ の個数を $ f(t) $ とおきます。 - $ i = 1, \dots, n $ に対し、頂点 $ p_i $ と頂点 $ p_{i + 1} $ を結ぶ単純パスに含まれる辺が $ 2 $ 本以下 (ただし、 $ p_{n + 1} = p_1 $ とする) --- 正整数 $ N, K $ 、および頂点に $ 1 $ から $ N $ までの番号がついた $ N $ 頂点の木 $ T_0 $ が与えられます。 $ T_0 $ の $ i $ 番目の辺は頂点 $ A_i $ と頂点 $ B_i $ を結びます。 $ T_0 $ を $ K $ 個つなげて得られる木を **良い木** と呼びます。 より形式的には、頂点に $ 1 $ から $ NK $ までの番号がついた $ NK $ 頂点の木 $ T $ が以下の条件を満たすとき、またそのときに限り $ T $ を良い木であるとします。 - $ 1\le i\le N - 1 $ かつ $ 0\le k\le K - 1 $ を満たすすべての整数の組 $ (i, k) $ に対し、頂点 $ (A_i + N\times k) $ と頂点 $ (B_i + N\times k) $ の間に辺が存在する すべての良い木 $ T $ に対する $ f(T) $ の総和を $ 998244353 $ で割った余りを求めてください。 $ Q $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。

入力は以下の形式で標準入力から与えられる。 > $ Q $ $ \mathrm{case}_1 $ $ \vdots $ $ \mathrm{case}_Q $ $ \mathrm{case}_i $ は以下の形式である。 > $ N $ $ K $ $ A_1 $ $ B_1 $ $ \vdots $ $ A_{N - 1} $ $ B_{N - 1} $

$ Q $ 行出力せよ。 $ i $ 行目には $ \mathrm{case}_i $ に対する答えを出力せよ。

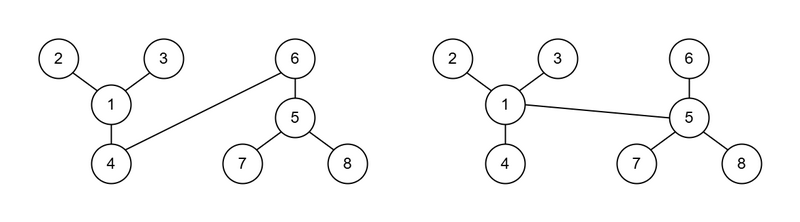
### Sample Explanation 1 $ 1 $ つ目のテストケースについて、どの単純パスも $ 2 $ 本以下の辺しか含まないため、ありうる順列が全て数えられます。 $ 2 $ つ目のテストケースについて、数える順列は $ (1, 2, 4, 3), $ $ (1, 3, 4, 2), $ $ (2, 1, 3, 4), $ $ (2, 4, 3, 1), $ $ (3, 1, 2, 4), $ $ (3, 4, 2, 1), $ $ (4, 2, 1, 3), $ $ (4, 3, 1, 2) $ の $ 8 $ 通りです。 $ 3 $ つ目のテストケースについて、すべての $ 4 $ 頂点の木 $ T $ に対する $ f(T) $ の総和を求める必要があります。 $ T_0 $ が辺を持たない場合があることに注意してください。 $ 4 $ つ目のテストケースについて、良い木として例えば以下のような木が挙げられます。  ### Constraints - $ 1\le Q\le 2\times 10 ^ 5 $ - $ 1\le N\le 2\times 10 ^ 5 $ - $ 1\le K\le 2\times 10 ^ 5 $ - $ 1\le A_i\lt B_i\le N $ - $ 1 $ つの入力ファイルに含まれる $ N $ の総和は $ 2\times 10 ^ 5 $ 以下 - 入力されるグラフは木 - 入力はすべて整数