AT_tupc2024_i Small Steps
题目描述
对于一个包含 $n$ 个顶点、顶点编号为 $1$ 到 $n$ 的树 $t$,我们定义满足下列条件的排列 $p = (p_1, \dots, p_n)$($p$ 是 $(1, \dots, n)$ 的一个排列)有多少个,记作 $f(t)$。
- 对于 $i = 1, \dots, n$,连接顶点 $p_i$ 和顶点 $p_{i+1}$ 的最短简单路径所经过的边数不超过 $2$(这里规定 $p_{n+1} = p_1$)。
---
给定正整数 $N, K$ 以及顶点编号为 $1$ 到 $N$ 的 $N$ 个顶点的树 $T_0$。$T_0$ 的第 $i$ 条边连接顶点 $A_i$ 和顶点 $B_i$。
将 $K$ 个 $T_0$ 连接起来所得的树称为**好树**。更为正式地说,当且仅当顶点编号为 $1$ 到 $NK$ 的 $NK$ 个顶点的树 $T$ 满足以下条件时,$T$ 是好树:
- 对于所有满足 $1 \le i \le N-1$ 且 $0 \le k \le K-1$ 的整数对 $(i, k)$,$T$ 包含一条边连接顶点 $(A_i + N\times k)$ 和顶点 $(B_i + N\times k)$。
请你求出所有好树 $T$ 的 $f(T)$ 之和对 $998244353$ 取模的结果。
有 $Q$ 组测试数据,请你分别输出答案。
输入格式
输入以如下格式从标准输入读入。
> $Q$
> $\mathrm{case}_1$
> $\vdots$
> $\mathrm{case}_Q$
每组 $\mathrm{case}_i$ 输入格式如下:
> $N$ $K$
> $A_1$ $B_1$
> $\vdots$
> $A_{N-1}$ $B_{N-1}$
输出格式
输出共 $Q$ 行。第 $i$ 行输出第 $i$ 组测试数据的答案。
说明/提示
### 样例说明 1
对于第 1 个测试点,由于所有简单路径都只包含至多 2 条边,因此所有可能的排列均被计数。
对于第 2 个测试点,被计数的排列共有 $8$ 种,分别是 $(1, 2, 4, 3)$、$(1, 3, 4, 2)$、$(2, 1, 3, 4)$、$(2, 4, 3, 1)$、$(3, 1, 2, 4)$、$(3, 4, 2, 1)$、$(4, 2, 1, 3)$、$(4, 3, 1, 2)$。
对于第 3 个测试点,需要求所有 $4$ 个顶点的树 $T$ 的 $f(T)$ 的总和。注意 $T_0$ 可能不含任何边。
对于第 4 个测试点,作为好树的例子,如下图所示:
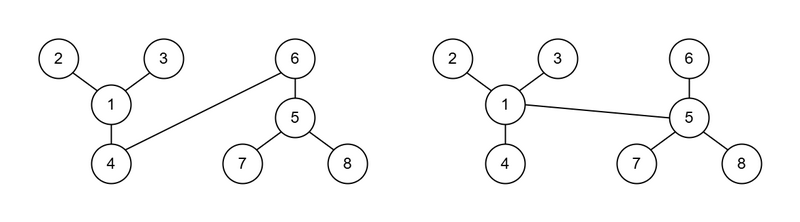
### 数据范围
- $1\le Q\le 2\times 10 ^ 5$
- $1\le N\le 2\times 10 ^ 5$
- $1\le K\le 2\times 10 ^ 5$
- $1\le A_i < B_i \le N$
- 所有输入文件中 $N$ 的总和不超过 $2\times 10^5$
- 输入给定的图均为树
- 输入全部为整数
由 ChatGPT 5 翻译