AT_utpc2013_04 壊れかけのヒープ

うなぎ王国のお姫様は，データ構造が大好きだ．そこで王様は，お姫様の誕生日に「バイナリヒープを表現した配列」をたくさんプレゼントしようと準備していた． 「バイナリヒープを表現した配列」とは，配列の第 $i$ 要素の値は，第 $2i+1$ 要素が存在すればそれより真に小さく，同様に第 $2i+2$ 要素が存在すればそれよりも真に小さい，という条件を全ての要素で満たす配列のことを言う．たとえば $[0,1,4,2,3]$ はバイナリヒープを表現した配列である．なぜならば，第 $0$ 要素である $0$ は第 $1$ 要素と第 $2$ 要素である $1$ と $4$ よりも小さく，第 $1$ 要素である $1$ は第 $3$ 要素と第 $4$ 要素の $2$ と $3$ よりも小さい…，という条件がすべて成り立っている．このような配列は，第 $i$ 要素の子が第 $2i+1$ 要素と第 $2i+2$ 要素であるようなツリー構造と考えると，親の方が常に値が小さいという特徴を持つ．お姫様は，この特徴を活用してソートなど様々なアルゴリズムの効率化をするのにご執心なのだ．  $$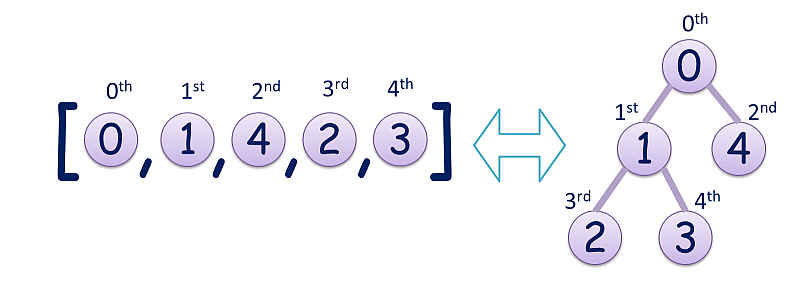図 1: 「バイナリヒープを表現した配列」の例$$ さて，ところが不運なことに，王様はせっかく作った「バイナリヒープを表現した配列」を落として壊してしまった！今や王様の手元には，「バイナリヒープを表現した配列」の後半部分しか手元に残っていない．一刻も早く元の「バイナリヒープを表現した配列」を復元しなくてはならない．王様は，元の配列の要素はすべて非負整数で，重複する値はなかったことを覚えている．この情報を手がかりに配列を復元して欲しい．

[problemUrl]: https://atcoder.jp/contests/utpc2013/tasks/utpc2013_04 すなわち，入力 $A_0...A_{N−1}$ に対し，次を満たす配列 $H_0...H_{M−1}$ を求め，その長さ $M$ を答えとして出力して欲しい． - $H_i$ は全て $0$ 以上の整数 - 配列の要素は全て互いに異なる．つまり，$i\neq j$ ならば $H_i\neq H_j$ - バイナリヒープを表現した配列となっている．つまり，常に $H_i

入力は以下の形式で与えられる． > $N$ $A_0$ $A_1\cdots A_{N-1}$

問題の解を $1$ 行に出力せよ．

入力中の各変数は以下の制約を満たす． - $1\leq N\leq 100$ - $0 \leq A_{i} \leq 10^9$ - $A_i$ は互いに相異なる非負整数