AT_utpc2024_j Journey through the Fractal

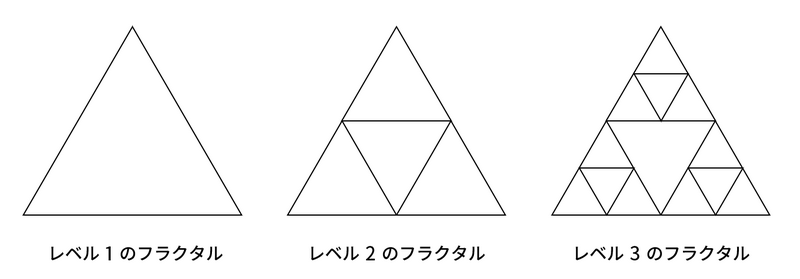
$ 1 $ 辺の長さが $ 2^{i-1} $ の正三角形を、**レベル** $ i $ **の三角形**と呼びます。また、次の規則にしたがって生成される図形を、**レベル** $ i $ **のフラクタル**と呼びます。 - レベル $ 1 $ のフラクタルは、レベル $ 1 $ の三角形である - レベル $ i + 1 $ $ (i \geq 1) $ のフラクタルは、レベル $ i $ の三角形の $ 3 $ 辺のそれぞれにぴったり接するように、レベル $ i $ のフラクタルを配置した図形である（詳しくは、図を参照してください）  ここに、レベル $ L $ のフラクタルがあります。 Alice は、まず初めに、フラクタルを構成する三角形のうち好きなものを $ 1 $ つ選び、その三角形からスタートします。その後、まだ訪れていない三角形であって、今いる三角形に辺で隣接するものがあれば $ 1 $ つ選び、移動します。 Alice は移動を $ K $ 回まで行うことができます。Alice が訪れた三角形（スタートした三角形も含む）のレベルの総和を、**スコア**と定めます。 スコアとしてありうる値の最大値を $ 998244353 $ で割った余りを求めてください。なお、 $ 998244353 $ で割った余りの最大値を求めるのではないことに注意してください。

入力は以下の形式で標準入力から与えられる。 > $ L $ $ K $

スコアの最大値を $ 998244353 $ で割った余りを出力せよ。

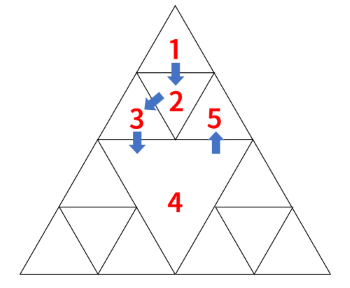
### Sample Explanation 1 図のように移動することで、レベル $ 1 $ の三角形を $ 4 $ つ、レベル $ 2 $ の三角形を $ 1 $ つ訪れることができます。 なお、図の三角形の中に書かれている数は、その三角形を何番目に訪れたかを表します。  ### Sample Explanation 2 スコアの最大値を $ 998244353 $ で割った余りを出力してください。 ### Constraints - 入力は全て整数 - $ 1 \leq L \leq 10^9 $ - $ 1 \leq K \leq 10^{18} $