AT_utpc2024_j Journey through the Fractal
题目描述
边长为 $2^{i-1}$ 的正三角形被称为**等级 $i$ 的三角形**。此外,按照以下规则生成的图形被称为**等级 $i$ 的分形**。
- 等级 $1$ 的分形是等级 $1$ 的三角形。
- 等级 $i+1$ $(i \geq 1)$ 的分形,是把 $3$ 个等级 $i$ 的分形分别紧贴等级 $i$ 的三角形的三条边排列而成的图形(详见下图)。
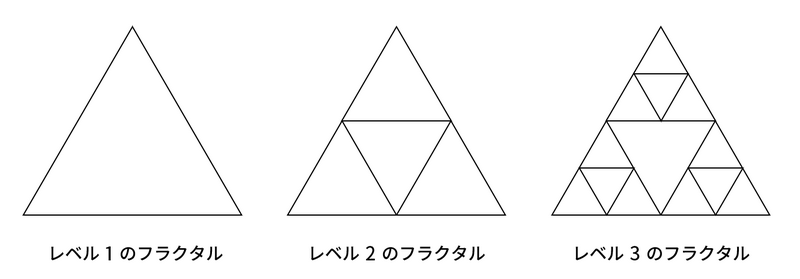
现在,给定一个等级为 $L$ 的分形。
Alice 首先可以任选组成分形的一个三角形,从该三角形开始。之后,她可以从当前所处的三角形,选择尚未访问过且与当前三角形通过边相邻的三角形,移动到该三角形。
Alice 最多可以移动 $K$ 次。Alice 访问过的所有三角形(包含起始三角形)对应等级的总和,定义为**得分**。
请你求出可能的得分的最大值,并将其对 $998244353$ 取余后的结果输出。请注意,这里的取余是对最大得分取模,而不是最大余数。
输入格式
输入从标准输入读取,格式如下:
> $L$ $K$
输出格式
请输出得分的最大值对 $998244353$ 取余的结果。
说明/提示
### 样例解释 1
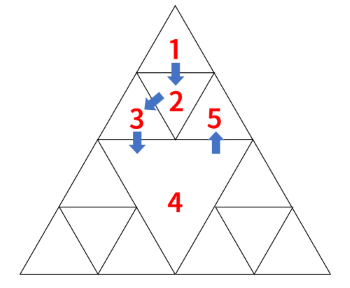
如下图所示,移动路径可以访问 $4$ 个等级 $1$ 的三角形和 $1$ 个等级 $2$ 的三角形。
图中三角形中的数字表示访问的顺序。
### 样例解释 2
请输出得分最大值对 $998244353$ 取余的结果。
### 数据范围
- 输入均为整数
- $1 \leq L \leq 10^9$
- $1 \leq K \leq 10^{18}$
由 ChatGPT 5 翻译