AT_utpc2024_p Perfect Suika Game on a Tree

$ 1 $ から $ N $ までの番号が付いた $ N $ 頂点からなる木 $ T $ があります。 $ i $ 番目の辺は頂点 $ u_i,v_i $ を結びます。 各頂点には**レベル**と呼ばれる正整数が割り当てられています。はじめ、各頂点 $ v = 1,2,\dots,N $ のレベルは $ A_v $ です。 木 $ T $ について、以下の問題を考えます。 > 木 $ T $ に対し以下のような操作をちょうど $ N-1 $ 回行うことで、 $ T $ を $ 1 $ 頂点のみからなる木にすることができるか判定してください。 - 両端点の頂点のレベルが等しいような辺を $ 1 $ つ選び、選んだ辺について縮約を行う。両端点の頂点のレベルを $ l $ としたとき、縮約により生じる新たな頂点のレベルを $ l+1 $ とする。 クエリが $ Q $ 個与えられるので処理してください。 $ i $ 番目のクエリでは辺番号 $ e_i $ が与えられるので、木 $ T $ における頂点 $ u_{e_i},v_{e_i} $ のレベルをスワップした後（このスワップの影響は以降のクエリにも残存します）、上記の問題の答えを出力してください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ $ \vdots $ $ u_{N-1} $ $ v_{N-1} $ $ A_1 $ $ A_2 $ $ \dots $ $ A_N $ $ Q $ $ e_1 $ $ e_2 $ $ \vdots $ $ e_Q $

$ Q $ 行出力せよ。 $ i $ 行目には $ i $ 番目のクエリについてレベルのスワップを行った後、上記の問題について、 $ T $ を $ 1 $ 頂点のみからなる木にすることができる場合 `Yes` を、できない場合 `No` を出力せよ。

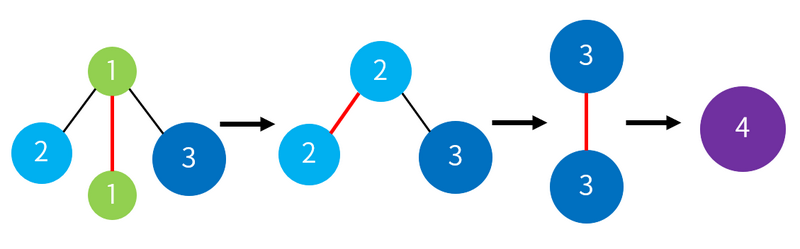
### 部分点 - 追加の制約 $ Q=1 $ を満たすデータセットに正解した場合は $ 20 $ 点が与えられる。 なお、以下で与えられるサンプルケースはいずれも部分点のデータセットに含まれない。 ### Sample Explanation 1 $ 1 $ 番目のクエリについて、頂点 $ u_1=1, v_1=2 $ のレベルのスワップを行った後、頂点 $ 1,2,3,4 $ のレベルはそれぞれ $ 1,1,2,3 $ になります。 この場合、下図のように赤く表示されている辺を選んで操作を行うことで、レベル $ 4 $ の頂点 $ 1 $ つからなる木にできます（下図において頂点に書かれている整数は頂点のレベルを示しています）。  よって $ 1 $ 行目には `Yes` を出力します。 $ 2 $ 番目のクエリについて、頂点 $ u_2=1, v_2=3 $ のレベルのスワップを行った後、頂点 $ 1,2,3,4 $ のレベルはそれぞれ $ 2,1,1,3 $ になります。 この場合、操作を $ 1 $ 度も行うことができず、 $ 1 $ つの頂点からなる木に変換することはできません。 よって $ 2 $ 行目には `No` を出力します。 ### Constraints - 入力はすべて整数 - $ 2 \leq N \leq 2 \times 10^5 $ - $ 1 \leq u_i,v_i \leq N $ - $ 1 \leq A_i \leq N $ - $ 1 \leq Q \leq 2 \times 10^5 $ - $ 1 \leq e_i \leq N-1 $ - 与えられるグラフは木