AT_utpc2024_p Perfect Suika Game on a Tree

有一棵包含 $N$ 个结点的树 $T$，结点编号为 $1$ 到 $N$。第 $i$ 条边连接结点 $u_i$ 和 $v_i$。 每个结点被分配了一个称为**等级**的正整数。初始时，每个结点 $v=1,2,...,N$ 的等级为 $A_v$。 考虑如下与树 $T$ 相关的问题： > 判断是否可以通过恰好进行 $N-1$ 次如下操作，把树 $T$ 最终变成仅含 $1$ 个结点的树。 - 每次选择一条其两个端点等级相同的边，对该边进行缩并。设该边的两个端点等级为 $l$，缩并后新结点的等级为 $l+1$。 现在有 $Q$ 个询问。第 $i$ 个询问会给出边的编号 $e_i$，请将树 $T$ 中与该边关联的两个结点 $u_{e_i}$ 和 $v_{e_i}$ 的等级交换（该交换对后续所有操作均生效），然后对上述问题给出答案。

输入按如下格式从标准输入读入。 > $N$ > $u_1\ v_1$ > $u_2\ v_2$ > $\vdots$ > $u_{N-1}\ v_{N-1}$ > $A_1\ A_2\ \dots\ A_N$ > $Q$ > $e_1$ > $e_2$ > $\vdots$ > $e_Q$

输出 $Q$ 行。第 $i$ 行输出对于第 $i$ 个询问，在等级交换操作后，是否能将树 $T$ 变为仅含 $1$ 个结点的树。若可以则输出 `Yes`，否则输出 `No`。

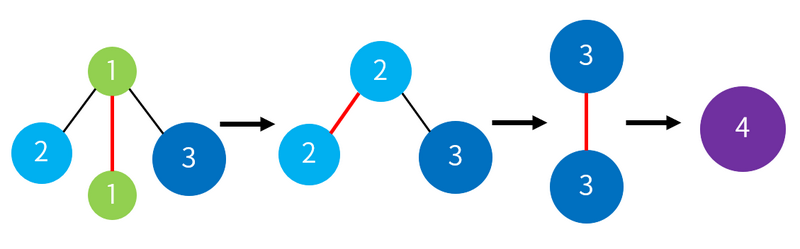
### 部分分 - 若能正确解决 $Q=1$ 的数据集，可得 $20$ 分。 此外，下面给出的样例不在部分分数据集中。 ### 样例解释 1 对于第 $1$ 个询问，在进行结点 $u_1=1, v_1=2$ 等级交换操作后，各结点 $1,2,3,4$ 的当前等级依次为 $1,1,2,3$。 此时可以如图中红色边所示进行操作，最终得到仅含一个等级为 $4$ 的结点的树（下图中结点编号所示的数字即结点的等级）。  因此第 $1$ 行输出 `Yes`。 对于第 $2$ 个询问，在进行结点 $u_2=1, v_2=3$ 的等级交换后，各结点 $1,2,3,4$ 的等级依次变为 $2,1,1,3$。 此时无法进行任意一次操作，无法将树变为一个结点。 因此第 $2$ 行输出 `No`。 ### 数据范围 - 所有输入均为整数。 - $2\leq N\leq 2\times 10^5$ - $1\leq u_i, v_i \leq N$ - $1\leq A_i \leq N$ - $1\leq Q\leq 2\times 10^5$ - $1\leq e_i\leq N-1$ - 给定的图保证为一棵树。 由 ChatGPT 5 翻译