AT_wupc_03 至高のケーキ

今天注定又是某个人的生日。在这里，我们有一个关于不喜欢草莓的人的生日蛋糕切分问题。想象一个生日蛋糕被制作成 $N$ 行 $M$ 列，每个单元是一个小正方形，代表蛋糕的一部分，每个部分都有一个称为“效用”的数值，表示某人在享用这部分蛋糕时能获得的满意度。最终，他从这些切分的小方块中获得的满意度是其效用值的总和。此外，蛋糕中有些部分可能含有草莓。 我们用字符串来表示这个蛋糕。蛋糕的每个部分用一个字符标识，其中： ``` 0, 1, 2, ..., 9 : 表示该部分可获得的效用值 X : 表示这部分含有草莓 ``` 现在，我们的任务是将蛋糕切成他喜欢的一种形状：阶梯状。阶梯状就像图 1 所示，单独的正方形也算是阶梯状。但是，由于他特别讨厌草莓，因此在切分时不能包含有草莓的部分。举例来说，如图 2 所示的切分方法就是无效的，因为包含了草莓。 根据给定的蛋糕效用值和草莓的位置，请计算他能够获得的最大满意度。 --- 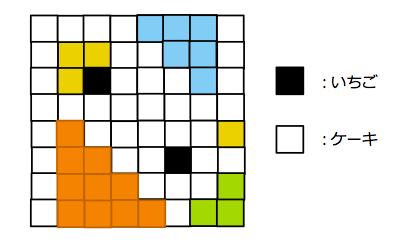 图 1: 可行的阶梯状切分 --- 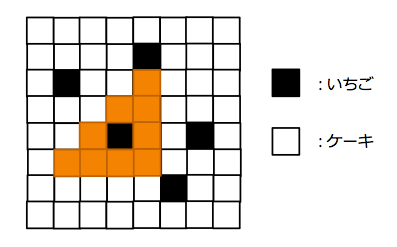 图 2: 无效的切分示例 --- ### 输入格式 - 第一行两个整数 $N$ 和 $M$（$1 \le N \le 30$，$1 \le M \le 30$），表示蛋糕的大小。 - 接下来的 $N$ 行每行包含一个长度为 $M$ 的字符串，表示蛋糕各部分的效用值或草莓的位置。 - 字符仅可能是 '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'X'，分别对应之前的效用值或草莓标识。 - 假设蛋糕中不会出现全部是草莓的情况，即 'X' 的数量小于 $N \times M$。 ### 输出格式 - 输出一个整数，表示他能获得的最大满意度。最后输出时请包含一个换行。 ### 数据范围与提示 - $1 \le N \le 30$ - $1 \le M \le 30$ 示例输入 1： ```plaintext 3 3 433 333 333 ``` 示例输出 1： ```plaintext 19 ``` 示例输入 2： ```plaintext 3 5 11111 1X1X1 11111 ``` 示例输出 2： ```plaintext 3 ``` **本翻译由 AI 自动生成**

无

无