AT_xmascon17_i SAT Puzzle

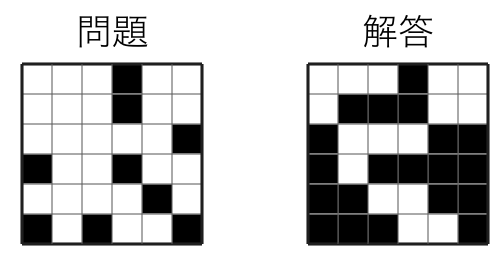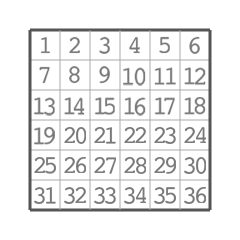[problemUrl]: https://atcoder.jp/contests/xmascon17/tasks/xmascon17_i 以下のパズルをSATで解いてください。 - $ 6*6 $ のマス目が与えられる。いくつかのマスは黒マスであり、それ以外は白マスである。 - 白マスをいくつか黒マスに変え、以下の条件を満たすようにせよ。 - 白マスの連結成分がちょうど $ 4 $ つ存在し、いずれもサイズは $ 4 $ である。 下図の例題も参考にしてください。 図１：例題 後々のためにマスには以下のように番号をつけておきます。 図２：マスの番号付け #### 解答方法 あなたはこのパズルを解くための以下のような[CNF](https://ja.wikipedia.org/wiki/%E9%80%A3%E8%A8%80%E6%A8%99%E6%BA%96%E5%BD%A2)を提出してください。 - 論理変数は $ x_1,\ x_2,\ ...,\ x_{1000} $ のみを用いる。 - 式を充足する真偽値の割り当てに対し、$ x_i\ (1\ \leq\ i\ \leq\ 36) $ がパズルの解答の盤面におけるマス $ i $ の色を表す。$ x_i $ が真の場合マス $ i $ は黒であり、偽の場合は白である。 #### ジャッジ方法 ジャッジは以下のように行われます。 - 提出のCNFに以下のような節を追加する。 - テストケースのパズルの初期盤面でマス $ i $ が黒く塗られているとき、$ (x_i) $ という節を追加する。（これにより、$ x_i $ は必ず真となる。） - CNFの充足可能性を判定する。充足不可能であった場合ジャッジ結果は `WA` となる。また、この判定に $ 30 $ 秒以上かかった場合は `IE` となる。 - 充足可能な場合は真偽値の割り当てを $ 1 $ つ見つけ、各 $ i\ (1\ \leq\ i\ \leq\ 36) $ について、$ x_i $ が真の場合マス $ i $ を黒マスにし、偽の場合は白マスにする。 - 得られた盤面がパズルの解として正しいかどうかを判定する。正しければジャッジ結果は `AC` となり、正しくなければ `WA` となる。 テストケースは $ 10 $ ケースあり、全てに正解すると `AC` となります。 [こちらのgist](https://gist.github.com/snuke/6635dd1ef944112ba5195856c4555bb4) にジャッジのソースコードをuploadしてあるので、デバッグ等にご利用ください。

この問題では入力は与えられない。

$ i $ 行目に $ i $ 番目の節の情報を出力し、最後の行に $ 0 $ を出力せよ。 各節の出力方法は [minisat](https://www.dwheeler.com/essays/minisat-user-guide.html) を参考にせよ。 例えば $ (x_1\ \lor\ x_2)\ \land\ (\lnot\ x_1\ \lor\ x_2\ \lor\ \lnot\ x_3) $ というCNFの場合は以下のように出力すれば良い。 ``` 1 2 0 -1 2 -3 0 0 ``` #### 注意点 以下の点に注意せよ。 - リテラルには $ x_1 $ から $ x_{1000} $ までしか使ってはいけない - 空の節を入れてはならない。（$ 0 $ のみが行に出力され、出力の終端だと判定されてしまうため）