AT_xmascon17_i SAT Puzzle

请通过 SAT 满足性解决以下谜题。 - 给定一个 $6 \times 6$ 的网格，其中部分格子是黑格子，其余的是白格子。 - 你需要将一些白格子转变为黑格子，使其满足以下条件： - 网格中有且只有 $4$ 个白色区域，每个区域都包含 $4$ 个连通的白格子。 请参考下图中的示例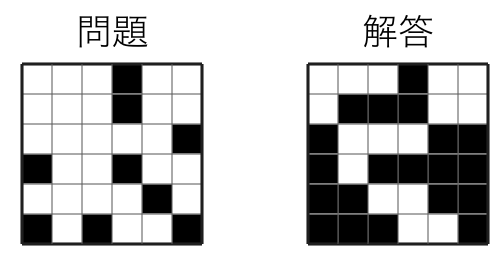：  图 1：示例 为了便于描述，我们对网格进行了如下编号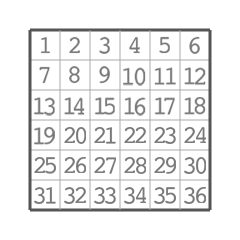：  图 2：格子编号 ## 解答格式 你的任务是提供这个谜题的一种 CNF 形式的解答。 - 仅允许使用逻辑变量 $x_1, x_2, \ldots, x_{1000}$。 - 满足 CNF 的真值赋值中，$x_i\ (1 \leq i \leq 36)$ 代表格子 $i$ 的颜色。$x_i$ 为真时表示格子 $i$ 是黑色，$x_i$ 为假时表示白色。 ## 判题标准 判题过程如下： - 在你提交的 CNF 中，针对于测试用例的初始黑格子，加入子句 $(x_i)$。这使得 $x_i$ 必须为真。 - 判断 CNF 的可满足性。如果不可满足，则结果为 `WA`，如果判断时间超过 $30$ 秒，则结果为 `IE`。 - 如果 CNF 是可满足的，则找到一个解，并根据解将 $x_i$ 为真的格子 $i$ 涂成黑色，$x_i$ 为假的涂成白色。 - 判断最后的网格状态是否为正确解答。如果是，结果为 `AC`，否则为 `WA`。 该题包含 $10$ 个测试用例，全部通过后判题结果为 `AC`。 可以使用 [此处提供的判题源代码](https://gist.github.com/snuke/6635dd1ef944112ba5195856c4555bb4) 进行调试。

この問題では入力は与えられない。

第 $i$ 行输出第 $i$ 个子句的信息，最后一行输出 $0$。子句的输出格式请参考 [minisat](https://www.dwheeler.com/essays/minisat-user-guide.html)。 例如，对于 CNF $(x_1 \lor x_2) \land (\lnot x_1 \lor x_2 \lor \lnot x_3)$，输出如下： ``` 1 2 0 -1 2 -3 0 0 ``` ### 注意事项 - 只能使用 $x_1$ 到 $x_{1000}$ 之间的逻辑变量。 - 不得包含空子句，即不能只输出 `0`，因为这将被视为输出的结束。 **本翻译由 AI 自动生成**