AT_xmascon19_i Stamps 4

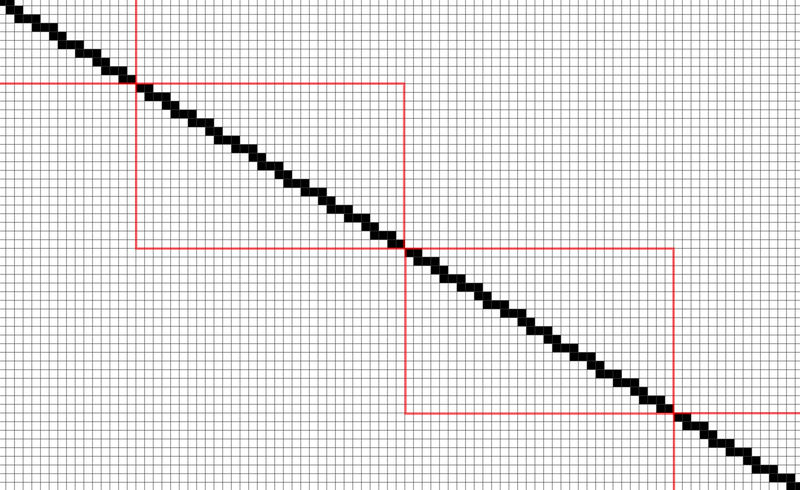
兔子有一个大小为 $H \times W$ 的矩形网格。在这个网格里，第 $i$ 行（$1 \le i \le H$）和第 $j$ 列（$1 \le j \le W$）的格子记作格子 $(i, j)$。 初始状态下，部分格子已经被涂成黑色。每个格子 $(i, j)$ 的状态通过字符 $S_{i,j}$ 来表示，其中 `#` 表示黑色，`.` 表示未被涂色。 兔子收到了一份圣诞礼物：一个印章。 使用这个印章一次可以将下图所示的格子区域全部涂成黑色。下图展示了一种由 $19 \times 31$ 的图案沿对角线无限重复构成的模式。但是这个印章只能以整格为单位进行平移，不能旋转、翻转或部分移动。  兔子想要利用这个印章将所有未涂色的格子全部变成黑色。你需要计算出最少需要盖印多少次才能实现这个目标。

输入通过标准输入给出，格式如下： 第一行是两个整数 $H$ 和 $W$，表示网格的行数和列数。 接下来的 $H$ 行中，每行有 $W$ 个字符，分别表示每个格子的状态。

输出一个整数，表示将所有格子涂成黑色所需的最小盖印次数。

- $1 \le H, W \le 1000$ - 每个 $S_{i,j}$ 是 `.` 或 `#`。 **本翻译由 AI 自动生成**