AT_xmascon19_i Stamps 4

[problemUrl]: https://atcoder.jp/contests/xmascon19/tasks/xmascon19_i うさぎは $ H\ \times\ W $ の長方形のマス目を持っている． マス目の上から $ i $ 行目 ($ 1\ \le\ i\ \le\ H $)，左から $ j $ 列目 ($ 1\ \le\ j\ \le\ W $) のマスをマス $ (i,j) $ と呼ぶ． 初め，いくつかのマスは黒く塗られている． マス $ (i,j) $ の情報は文字 $ S_{i,j} $ で表され，`#` は黒く塗られていること，`.` は塗られていないことを意味する． うさぎはクリスマスプレゼントとしてスタンプをもらった． このスタンプを $ 1 $ 回押すと下図のようなマスの集合を全て黒く塗ることができる． 下図についてより詳細に説明すると，赤枠で囲われた $ 19\ \times\ 31 $ のパターンを斜め一直線に無限につなげたものである． ただし，スタンプは下図を $ 1 $ マス単位で平行移動させて押すことしかできず，回転・反転させることや $ 0.5 $ マスずらして押すこと等はできない．  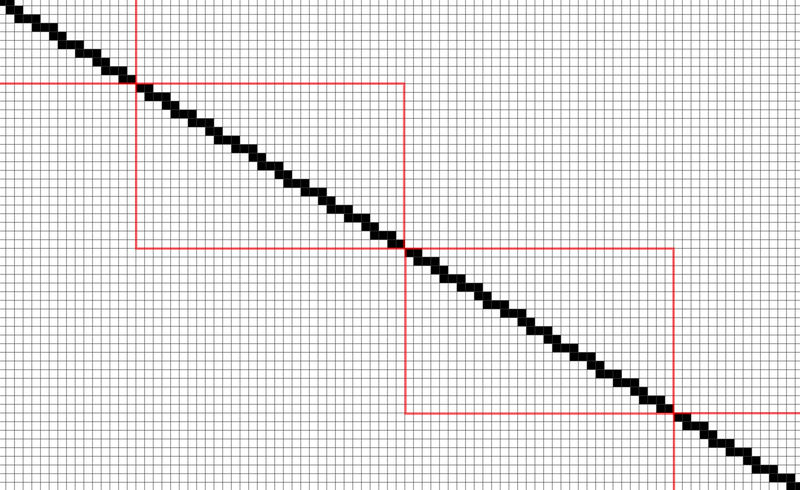うさぎはこのスタンプを使って，まだ塗られていないマスを全て黒く塗ろうとしている． 最小で何回スタンプを押せば良いだろうか？

入力は以下の形式で標準入力から与えられる． > $ H $ $ W $ $ S_{1,1} $$ S_{1,2} $$ ... $$ S_{1,W} $ $ S_{2,1} $$ S_{2,2} $$ ... $$ S_{2,W} $ $ : $ $ S_{H,1} $$ S_{H,2} $$ ... $$ S_{H,W} $

全てのマスが黒く塗られた状態にするためにスタンプを押す必要のある回数の最小値を出力せよ．

### 制約 - $ 1\ \le\ H,W\ \le\ 1000 $ - $ S_{i,j} $ は `.` または `#`