AT_xmascon19_k Set of Trees

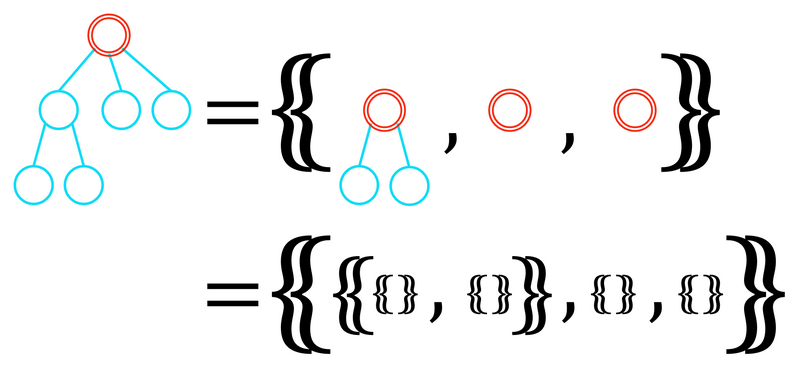[problemUrl]: https://atcoder.jp/contests/xmascon19/tasks/xmascon19_k **根付き木**を，「根付き木のある多重集合について，それらの根を新たな $ 1 $ 個の頂点と辺で結びその頂点を根としたもの」として再帰的に定義する (繋ぐときの並べ方を区別しないことに注意せよ)． 特に，$ 1 $ 頂点のみからなる木は空集合に対応する． この問題では，頂点数が有限の根付き木のみを考える． 根付き木 $ T_1,\ \ldots,\ T_k $ を新たな根に繋いだ根付き木を $ \{\!\!\{T_1,\ \ldots,\ T_k\}\!\!\} $ と書く． 例えば以下の図のようになる． 根付き木は根付き木の多重集合 根付き木 $ T,\ T' $ の順序を，「$ T_1\ \ge\ \cdots\ \ge\ T_k,\,\ T'_1\ \ge\ \cdots\ \ge\ T'_l $ によって $ T\ =\ \{\!\!\{T_1,\ \ldots,\ T_k\}\!\!\},\,\ T'\ =\ \{\!\!\{T'_1,\ \ldots,\ T'_l\}\!\!\} $ と表したとき， 列 $ s\ =\ (T_1,\ \ldots,\ T_k),\,\ s'\ =\ (T'_1,\ \ldots,\ T'_l) $ を辞書式順序で比較して， $ s\ \ s' $ ならば $ T\ >\ T' $」として再帰的に定義する ($ T\ \ge\ T' $ は $ T\ >\ T' $ または $ T\ =\ T' $ を表す)． 例えば以下の図のようになる． 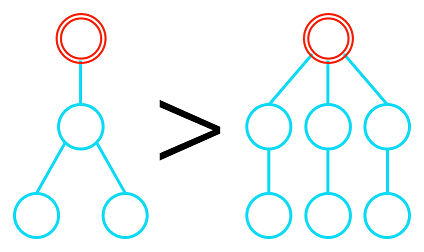根付き木の順序 くろうさとしろうさがゲームを行う． 盤面には根付き木がいくつかある． 最初，頂点は合計で $ N $ 個あり，$ 1 $ から $ N $ までの番号がついている． $ P_i\ =\ 0 $ のとき頂点 $ i $ は盤面の根付き木のうち $ 1 $ 個の根であり，$ P_i\ >\ 0 $ のとき頂点 $ i $ と頂点 $ P_i $ が辺で結ばれている． 先手くろうさと後手しろうさは交互に次の行動を行う：盤面にある根付き木を $ 1 $ 個選び，上で定めた順序でそれより真に小さい根付き木に書き換える (すなわち，選んだ根付き木を $ T $ とするとき，$ T\ >\ T' $ なる根付き木 $ T' $ を $ 1 $ 個選んで，選んだ部分を $ T' $ に変化させる)． 行動できなくなった側が負けであり，相手が負けたら勝ちである． くろうさもしろうさも，以下に従う． - 必ず勝つことができるならば，勝つように行動する． - 必ず勝つことはできないが必ず負けないようにできるならば，負けないように行動する． このときどちらが勝つか，あるいはゲームが無限に続くかを決定せよ．

> $ N $ $ P_1 $ $ ... $ $ P_N $

くろうさが勝つ場合 `Black` を，しろうさが勝つ場合 `White` を，ゲームが無限に続く場合 `Infinity` を出力せよ．

### 制約 - $ 1\ \le\ N\ \le\ 201912 $． - $ 0\ \le\ P_i\ \le\ i\ -\ 1 $ ($ 1\ \le\ i\ \le\ N $)． ### 部分点 - $ N\ \le\ 2019 $ を満たすデータセットに正解した場合は，$ 45 $ 点が与えられる． - 追加制約のないデータセットに正解した場合は，上記とは別に $ 55 $ 点が与えられる． ### Sample Explanation 1 くろうさは，初手で頂点 $ 3 $ を根とする部分木を図のように書き換えることで勝つことができる． !\[\](https://img.atcoder.jp/xmascon19/a7916b0147ae0bf46e9b2e8454fbd125.png)入力例 1