AT_xmascon19_k Set of Trees
题目描述
我们将**根树**递归地定义如下:从一组多重根树集合中,将这些根通过一个新的顶点和边连接起来,形成一个新的根树(注意,连接的顺序不影响结果)。特别地,仅包含一个顶点的树对应于空集合。在这个问题中,我们只讨论由有限个顶点组成的根树。记由根树 $T_1, \ldots, T_k$ 组成并连接的新根树为 $\{\!\!\{T_1, \ldots, T_k\}\!\!\}$。下面是一个例子的示意图:
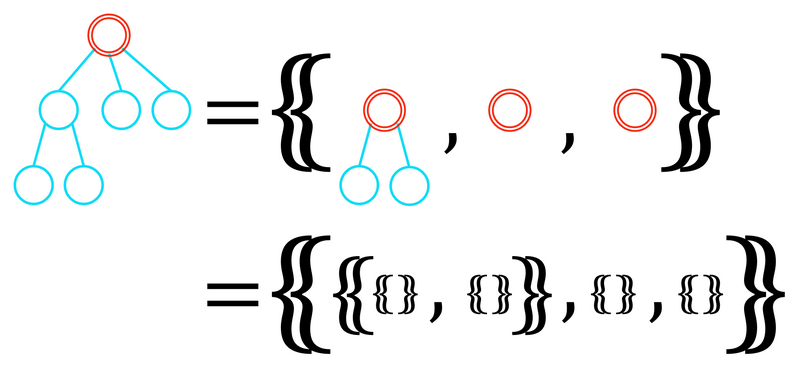
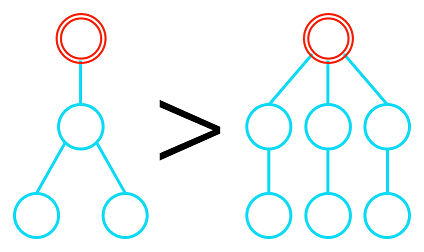
根树的顺序递归地定义为:对于根树 $T = \{\!\!\{T_1, \ldots, T_k\}\!\!\}$ 和 $T' = \{\!\!\{T'_1, \ldots, T'_l\}\!\!\}$,设 $T_1 \ge \cdots \ge T_k, T'_1 \ge \cdots \ge T'_l$。我们以字典序比较序列 $s = (T_1, \ldots, T_k)$ 和 $s' = (T'_1, \ldots, T'_l)$,若 $s < s'$,则 $T < T'$;若 $s = s'$,则 $T = T'$;若 $s > s'$,则 $T > T'$。($T \ge T'$ 表示 $T > T'$ 或 $T = T'$)。以下是一个示意图:
黑郎和白郎进行一个游戏。初始时,盘面上有若干棵根树,其中共 $N$ 个顶点,编号从 $1$ 到 $N$。如果 $P_i = 0$,则顶点 $i$ 为某棵树的根;如果 $P_i > 0$,则顶点 $i$ 与顶点 $P_i$ 有一条边相连。黑郎先手,二人交替执行以下操作:从盘面上选择一棵根树,并用比它严格小的另一棵根树替换之(即,选择一棵根树 $T$,然后选择一个 $T' < T$ 的根树替换 $T$)。无法继续操作的一方输掉游戏。
他们的策略如下:
- 如果可以确保胜利,则采取可确保胜利的策略。
- 如果无法确保胜利但可以避免失败,则采取避免失败的策略。
请判断这场游戏的结果:是黑郎赢,白郎赢,还是游戏会无限进行。
输入格式
输入包括两行。第一行是一个整数 $N$,表示顶点数。第二行是 $N$ 个整数 $P_1, P_2, \ldots, P_N$。
输出格式
如果黑郎赢,输出 `Black`;如果白郎赢,输出 `White`;如果游戏无限进行,输出 `Infinity`。
说明/提示
- $1 \le N \le 201912$。
- $0 \le P_i \le i - 1$($1 \le i \le N$)。
## 示例
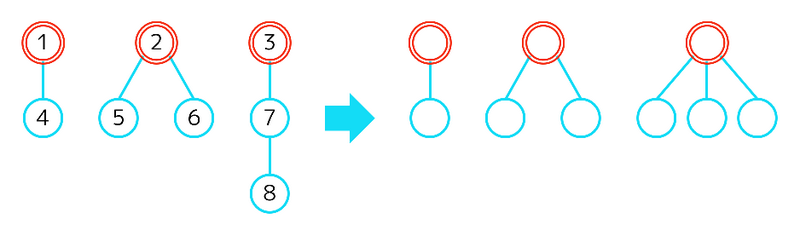
在第一个示例中,黑郎可以通过在第一步将顶点 $3$ 作为根的子树替换成如图所示的新根树来取得胜利。
**本翻译由 AI 自动生成**