AT_xmascon20_g Graph Products

[problemUrl]: https://atcoder.jp/contests/xmascon20/tasks/xmascon20_g この問題では，グラフは無向単純グラフのみを考える．グラフ $ H,\ H' $ に対し，グラフ $ H\ \mathbin{\square}\ H' $ と $ H\ \times\ H' $ を以下のように定義する．$ H,\ H' $ の頂点集合をそれぞれ $ V(H),\ V(H') $ と書く．$ W\ =\ V(H)\ \times\ V(H') $ (すなわち「$ H $ の頂点と $ H' $ の頂点の組」全体の集合) とおく． $ H\ \mathbin{\square}\ H' $ の頂点集合は $ W $ であり，$ H\ \mathbin{\square}\ H' $ において頂点 $ (u,\ u')\ \in\ W $ と $ (v,\ v')\ \in\ W $ を結ぶ辺があるための必要十分条件は，以下のいずれかが成り立つことである： - $ u\ =\ v $，かつ，$ H' $ において頂点 $ u' $ と頂点 $ v' $ を結ぶ辺がある． - $ u'\ =\ v' $，かつ，$ H $ において頂点 $ u $ と頂点 $ v $ を結ぶ辺がある． $ H\ \times\ H' $ の頂点集合は $ W $ であり，$ H\ \times\ H' $ において頂点 $ (u,\ u')\ \in\ W $ と $ (v,\ v')\ \in\ W $ を結ぶ辺があるための必要十分条件は，「$ H $ において頂点 $ u $ と頂点 $ v $ を結ぶ辺があり，かつ，$ H' $ において頂点 $ u' $ と頂点 $ v' $ を結ぶ辺があること」である． 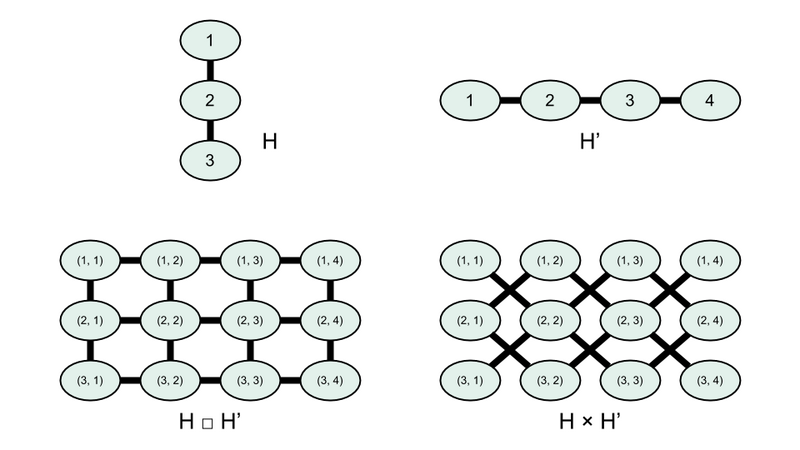例 $ K $ 個のグラフ $ G_1,\ \ldots,\ G_K $ が与えられる．各 $ k $ ($ 1\ \le\ k\ \le\ K $) に対し，$ G_k $ の頂点集合は $ \{1,\ \ldots,\ N_k\} $ であり，$ G_k $ は $ M_k $ 本の辺を持ちその $ i $ 番目 ($ 1\ \le\ i\ \le\ M_k $) は頂点 $ A_{k,i} $ と $ B_{k,i} $ を結ぶ． 各 $ k,\ k' $ ($ 1\ \le\ k\ \le\ K $，$ 1\ \le\ k'\ \le\ K $) に対し，グラフ $ G_k\ \mathbin{\square}\ G_{k'} $ と $ G_k\ \times\ G_{k'} $ が同型であるか判定せよ (すなわち，全単射 $ f\colon\ V(G_k)\ \times\ V(G_{k'})\ \to\ V(G_k)\ \times\ V(G_{k'}) $ であって，任意の $ (u,\ u'),\ (v,\ v')\ \in\ V(G_k)\ \times\ V(G_{k'}) $ に対し「$ G_k\ \mathbin{\square}\ G_{k'} $ において頂点 $ (u,\ u') $ と頂点 $ (v,\ v') $ を結ぶ辺があること」と「$ G_k\ \times\ G_{k'} $ において頂点 $ f((u,\ u')) $ と頂点 $ f((v,\ v')) $ を結ぶ辺があること」が同値となるようなものが存在するか判定せよ)．

入力は以下の形式で標準入力から与えられる． > $ K $ $ N_1 $ $ M_1 $ $ A_{1,1} $ $ B_{1,1} $ $ \vdots $ $ A_{1,M_1} $ $ B_{1,M_1} $ $ \vdots $ $ N_K $ $ M_K $ $ A_{K,1} $ $ B_{K,1} $ $ \vdots $ $ A_{K,M_K} $ $ B_{K,M_K} $

出力は $ K $ 行からなり，各行は $ K $ 文字からなる．$ k $ 行目 ($ 1\ \le\ k\ \le\ K $) の $ k' $ 文字目 ($ 1\ \le\ k'\ \le\ K $) には，$ G_k\ \mathbin{\square}\ G_{k'} $ と $ G_k\ \times\ G_{k'} $ が同型である場合は `1` を，同型でない場合は `0` を出力せよ．

### 制約 - $ 1\ \le\ K\ \le\ 10 $． - $ 1\ \le\ N_k\ \le\ 25\,000 $ ($ 1\ \le\ k\ \le\ K $)． - $ 0\ \le\ M_k\ \le\ 25\,000 $ ($ 1\ \le\ k\ \le\ K $)． - $ 1\ \le\ A_{k,i}\