AT_xmascon21_b Bad Mood

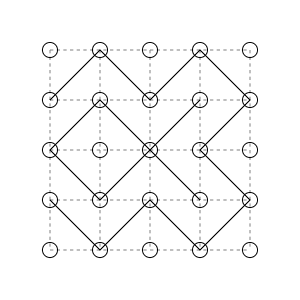[problemUrl]: https://atcoder.jp/contests/xmascon21/tasks/xmascon21_b 正の整数 $ M,\ N $ が与えられる．$ M $ 行 $ N $ 列のマス目があり，各マスは正方形である． これから，各マスに対角線のうちちょうど $ 1 $ つを書き込む．このとき，無向グラフであって，いずれかのマスの頂点であるような $ (M\ +\ 1)\ (N\ +\ 1) $ 個の点をグラフの頂点とし，書き込まれた対角線をグラフの辺とするものを考え，その連結成分の個数を書き込み方の**得点**と呼ぶ．得点としてあり得る最小値と最大値を求めよ． 得点が $ 10 $ となる例

入力は以下の形式で標準入力から与えられる． > $ M $ $ N $

得点としてあり得る最小値 $ a $ と最大値 $ b $ を以下の形式で出力せよ． > $ a $ $ b $

### 制約 - $ 1\ \le\ M\ \le\ 10^9 $． - $ 1\ \le\ N\ \le\ 10^9 $． ### Sample Explanation 1 得点が $ 6 $ となる例と得点が $ 7 $ となる例を以下の図に示す． !\[得点が $ 6 $ となる例\](https://img.atcoder.jp/xmascon21/105091090192bc5be451863d86ff441c.png)!\[得点が $ 7 $ となる例\](https://img.atcoder.jp/xmascon21/b293f4f8d17c9c01555ac5bc4d9c3b72.png)