AT_xmascon21_e E and PI

设 $e = 2.718\cdots$ 为自然对数的底数，$\pi = 3.141\cdots$ 为圆周率。 对于正整数 $n$，定义实数 $f(n)$ 如下：在坐标平面上，考虑以原点 $(0, 0)$ 为中心、半径为 $1$ 的圆 $C$。在 $C$ 上取点 $P_0, P_1, \ldots, P_{n-1}$，其中 $P_j$ 的坐标为 $(\cos(2\pi e j),\ \sin(2\pi e j))$（$j = 0, 1, \ldots, n-1$）。可以证明 $P_0, P_1, \ldots, P_{n-1}$ 互不相同，因此圆 $C$ 被这些点分成 $n$ 个弧。取这些弧中长度的最大值，记为 $f(n)$。 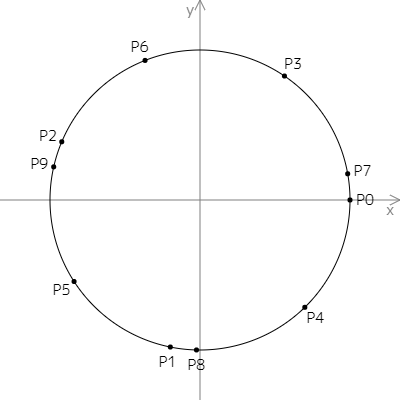 这是 $n = 10$ 时的示意图。 可以证明，满足 $f(n) > f(n+1)$ 的正整数 $n$ 有无穷多个。将这些 $n$ 按升序记为 $n_1, n_2, \ldots$。 给定正整数 $K$。可以证明，存在唯一的整数 $a, b$，使得 $f(n_K) = 2\pi(a + e b)$。请分别求 $n_K, a, b$ 对 $998244353$ 取余（即分别对 $998244353$ 取模，结果在 $0$ 到 $998244352$ 之间）。

输入为一行，包含一个整数 $K$。

请依次输出 $n_K, a, b$ 对 $998244353$ 取余的结果，用空格分隔。

### 数据范围 - $1 \leq K \leq 10^{11}$。 ### 样例解释 1 $n_1 = 1$，$f(1) = 2\pi$。 ### 样例解释 2 $n_2 = 2$，$f(2) = 2\pi(-2 + e)$。 ### 样例解释 3 $n_5 = 10$，$f(10) = 2\pi(-8 + 3e)$。 由 ChatGPT 4.1 翻译