AT_xmascon23_a Art Irrationnel

$ k = 2, 3, 4 $ のうち $ 1 $ つを選び，以下の問に答えよ． 横の長さと縦の長さの比が $ 1 : \left(1 + \sqrt[k]{2}\right) $ または $ \left(1 + \sqrt[k]{2}\right) : 1 $ であるような長方形を有限個，隙間や重なりなく並べて，正方形を作れ．より詳しい制限は「出力」のセクションを参照せよ． **[簡易的なビジュアライザがここから利用可能である．](https://hos.ac/contest/xmas2023/art_irrationnel.html)**

入力は空である．

以下の形式で出力せよ． > $ k $ $ r $ $ n $ $ a_1 $ $ b_1 $ $ c_1 $ $ d_1 $ $ a_2 $ $ b_2 $ $ c_2 $ $ d_2 $ $ \vdots $ $ a_n $ $ b_n $ $ c_n $ $ d_n $ - $ k $ はあなたが選んだ $ 2, 3, 4 $ のいずれかの値である． - 実数 $ r $ の形式は後述される．作った正方形が直交座標平面上の $ (0, 0), (r, 0), (r, r), (0, r) $ を $ 4 $ 頂点とすることを表す． - $ n $ は長方形の個数を表す． $ 1 \le n \le 10^5 $ を満たさなければならない． - 実数 $ a_i, b_i, c_i, d_i $ ( $ 1 \le i \le n $ ) の形式は後述される． $ i $ 個目の長方形が $ (a_i, c_i), (b_i, c_i), (b_i, d_i), (a_i, d_i) $ を $ 4 $ 頂点とすることを表す． - $ r $ および $ a_i, b_i, c_i, d_i $ ( $ 1 \le i \le n $ ) のそれぞれについて， $ k $ 個の整数 $ p_0, p_1, \ldots, p_{k-1} $ を空白区切りで出力せよ．これは値が $ \sum_{j=0}^{k-1} p_j \left(\sqrt[k]{2}\right)^j $ であることを表す． $ -10^9 \le p_j \le 10^9 $ を満たさなければならない． - $ r > 0 $ を満たさなければならない． - 各 $ 1 \le i \le n $ に対し， $ 0 \le a_i < b_i \le r $ かつ $ 0 \le c_i < d_i \le r $ を満たさなければならない． - 各 $ 1 \le i \le n $ に対し， $ \dfrac{d_i-c_i}{b_i-a_i} = 1 + \sqrt[k]{2} $ または $ \dfrac{b_i-a_i}{d_i-c_i} = 1 + \sqrt[k]{2} $ を満たさなければならない． - 正方形の内部および境界のすべての点は $ n $ 個の長方形のいずれかの内部および境界に含まれていなければならず， $ n $ 個の長方形のどの $ 2 $ つの内部も正の面積の共通部分を持ってはならない．

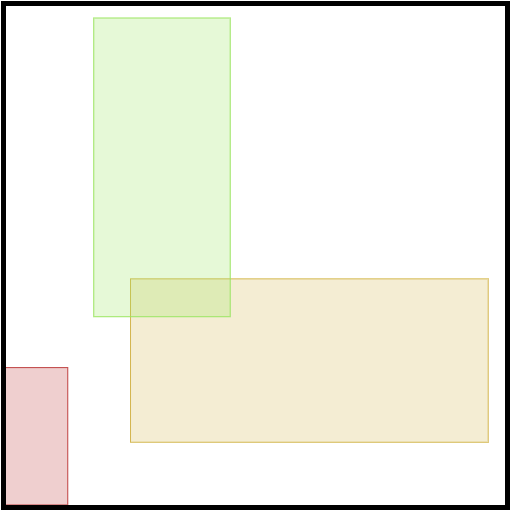### Sample Explanation 1 これは最後の条件**以外**を満たす出力である (よって，不正解と判定される)．この例では長方形は以下の図のように配置されている (座標は左下隅が $ (0, 0) $ ，右下隅が $ (r, 0) $ である)． 出力例 **[簡易的なビジュアライザがここから利用可能である．](https://hos.ac/contest/xmas2023/art_irrationnel.html)**